Cho ba số phức z 1 , z 2 , z 3 thỏa mãn điều kiện z 1 = z 2 = z 3 = 1 và z 1 + z 2 + z 3 = 0 . Tính A = z 1 2 + z 2 2 + z 3 2
A. 1
B. 0
C. -1
D. 1+i
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Em hãy thực hiện câu này theo cả 2 cách nhé!
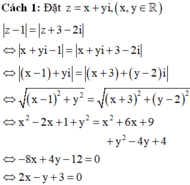
Vậy tập hợp các điểm biểu diễn số phức z là một đường thẳng có phương trình: 2x - y + 3 = 0
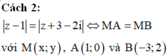
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
AB → = − 4 ; 2 , trung điểm của AB là I − 1 ; 1 , ∆ qua điểm I nhận AB → = − 4 ; 2 làm vectơ pháp tuyến.
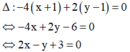
Đáp án A
Em hãy thực hiện Câu nay theo cả 2 cách nhé!
Cách 1: Đặt 
Cách 2: 
với M(x;y), A(1;0) và B(-3;2)
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực ∆ của đoạn thẳng AB như sau:
trung điểm của AB là I(-1;1),
∆
qua điểm I nhận 
làm vectơ pháp tuyến.
Đáp án A
Đặt z = x + yi với x,y ∈ ℝ , ta có:
= 5x - 5yi
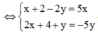
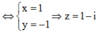
Do đó 
Vậy w có phần ảo bằng 2 1009
Chọn B.
Giả sử z = x + yi. Theo bài ra ta có: |x + 1 + (y – 2)i| = |x + 3 + (4 – y)i|
hay ( x + 1) 2+ ( y - 2) 2 = ( x + 3) 2 + ( y - 4) 2
suy ra y = x + 5
Số phức
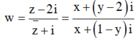
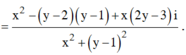
w là một số ảo
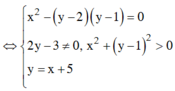
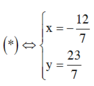
Vậy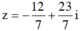 
Đáp án B
z 1 2 + z 2 2 + z 3 2 = z 1 + z 2 + z 3 2 - 2 ( z 1 z 2 + z 2 z 3 + z 3 z 1 = - 2 z 1 z 2 z 2 1 z 1 + 1 z 2 + 1 z 3 = - 2 z 1 z 2 z 2 z 1 z 1 + z 2 z 2 + z 3 z 3 = - 2 z 1 z 2 z 2 z 1 + z 2 + z 3 = 0