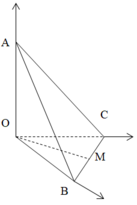
Cho khối tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và OA = OB = OC = 6. Tính bán kính R mặt cầu ngoại tiếp tứ diện OABC.
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Gọi M,N lần lượt là trung điểm của BC và OA
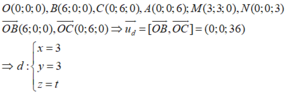
Gọi (P) là mặt phẳng trung trực của OA: z - 3 =0
Goi I là tâm mặt cầu ngoại tiếp tứ diện => I = P ∩ d ⇒ I 3 ; 3 ; 3 R = I A = 3 3

Đáp án D
Gọi M,N lần lượt là trung điểm của BC và OA
O ( 0 ; 0 ; 0 ) , B ( 6 ; 0 ; 0 ) , C ( 0 ; 6 ; 0 ) , A ( 0 ; 0 ; 6 ) ; M ( 3 ; 3 ; 0 ) , N ( 0 ; 0 ; 3 ) O B → ( 6 ; 0 ; 0 ) , O C → ( 0 ; 6 ; 0 ) ⇒ u d → = [ O B → , O C → ] = ( 0 ; 0 ; 36 ) ⇒ d : x = 3 y = 3 z = t
Gọi (P) là mặt phẳng trung trực của OA: z - 3 = 0
Goi I là tâm mặt cầu ngoại tiếp tứ diện

Đáp án D
Gọi M, N lần lượt là trung điểm của BC và OA
Gọi (P) là mặt phẳng trung trực của OA: z - 3 = 0
Goi I là tâm mặt cầu ngoại tiếp tứ diện
R = IA = 3 3