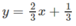Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi y = x 2 3 , x = 0 và tiếp tuyến với đường y = x 2 3 tại điểm có hoành độ x = 1, quanh trục Oy;
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Phương pháp:
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng x = a , x = b ( a < b ) và các đồ thị hàm số ư
y = f(x), y = g(x) khi quay quanh trục Ox là: V = π ∫ a b f 2 x - g 2 x dx
Cách giải:
Ta có công thức tính thể tích hình phẳng đã cho là:
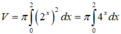

Đáp án B
y = 2 x + 1 1 3 ⇒ x = y 3 − 1 2 ; x = 0 ⇒ y = 1 Thể tích khối tròn xoay được tạo thành khi quay trục Oy hình phẳng gởi hạn bởi đồ thị hàm số y = 2 x + 1 1 3 đường thẳng y=3 và đường thẳng được tính bằng công thức V = π ∫ 1 3 y 3 − 1 2 2 d y = 480 π 7 .

Đáp án D
V = π ∫ 0 π 4 tan x . d x = π ∫ 0 π 4 sin x cos x . d x = π ∫ π 4 0 d cos x cos x . d x = π . ln cos x 0 π 4 = − π . ln 1 2 = π . ln 2

Đáp án D
Thể tích khối tròn xoay tạo thành khi quay phần mặt phẳng được giới hạn như hình vẽ (tô màu) quanh trục Ox là
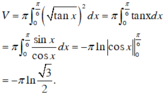
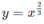 , x = 0 và tiếp tuyến với đường
, x = 0 và tiếp tuyến với đường 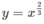 tại điểm có hoành độ x = 1, quanh trục Oy;
tại điểm có hoành độ x = 1, quanh trục Oy;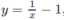 , y = 0, y = 2x, quanh trục Ox
, y = 0, y = 2x, quanh trục Ox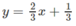
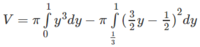
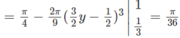
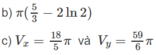

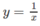
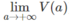
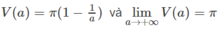
π /36.
Phương trình tiếp tuyến là: