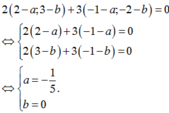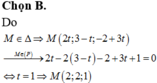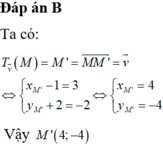Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(M\left(a;b\right)\)
\(\Rightarrow\overrightarrow{MB}=\left(2-a;3-b\right)\Rightarrow2\overrightarrow{MB}=\left(4-2a;6-2b\right)\)
\(\overrightarrow{MC}=\left(-1-a;-2-b\right)\Rightarrow3\overrightarrow{MC}=\left(-3-3a;-6-3b\right)\)
\(\Rightarrow2\overrightarrow{MB}+3\overrightarrow{MC}=\left(1-5a;-5b\right)=\overrightarrow{0}\)
\(\Rightarrow\left\{{}\begin{matrix}1-5a=0\\-5b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{1}{5}\\b=0\end{matrix}\right.\) \(\Rightarrow M\left(\frac{1}{5};0\right)\)
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
Đáp án B
Ta có: T v → ( M ) = M ' = M M ' → = v → ⇔ x M ' - 1 = 3 y M ' + 2 = - 2 ⇔ x M ' = 4 y M ' = - 4 . Vậy M'(4;-4)
