Bác Ba Phi có một mảnh vườn hình tam giác ABC với AB = 30m, AC = 40m và BC = 50m. Bác muốn đào một cái ao hình chữ nhật trên mảnh vườn này bằng cách chọn một điểm P trên cạnh BC rồi hạ các đường vuông góc PQ, PR lần lượt xuống AB, AC hình thành hình chữ nhật AQPR. Hỏi phải chọn điểm P cách B bao nhiêu mét để hình chữ nhật có diện tích lớn nhất? Diện tích lớn nhất đó bằng bao nhiêu mét vuông?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

6 tháng 3 2023
a: Chiều rộng là 50-20=30m
S vườn=50*30=1500m2
b: Diện tích ao là 5^2=25m2
S nền đất=25*4=100m2
Ao được đào sâu:
25:100*5=1,25(m)

CM
7 tháng 10 2019
Chọn B.
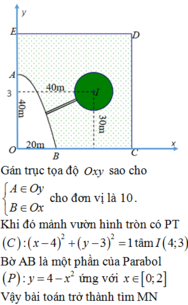
Phương pháp: Sử dụng phương pháp tọa độ trong mặt phẳng.
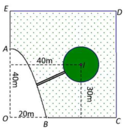
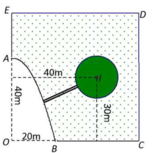
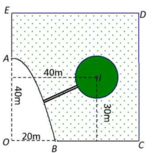
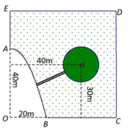
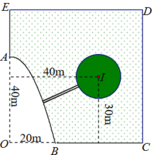
Cách giải: Chọn hệ trục tọa độ Đề các vuông góc như sau:
Gốc O, chiều dương trục hoành là tia OC, chiều dương trục tung là tia OE, đơn vị hai trục là đơn vị độ dài 1m
Khi đó ta có phương trình Parabol là

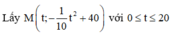
nằm trên Parabol thì khoảng cách ngắn nhất từ đường tròn đến M là
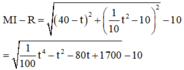
Khảo sát hàm số suy ra khoảng cách ngắn nhất xấp xỉ 17,7

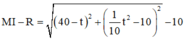
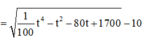
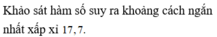
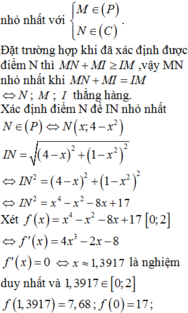

Pitago đảo \(\Rightarrow\Delta ABC\) vuông tại A
Ta có: \(PQ||AC\) (cùng vuông góc AB)
\(\Rightarrow\dfrac{PQ}{AC}=\dfrac{BP}{BC}\)
Tương tự: \(\dfrac{PR}{AB}=\dfrac{CP}{BC}\)
\(\Rightarrow\dfrac{PQ.PR}{AB.AC}=\dfrac{BP.CP}{BC^2}\)
\(\Rightarrow PQ.PR=\dfrac{30.40}{50^2}.BP.CP=\dfrac{12}{25}BP.CP\le\dfrac{3}{25}\left(BP+CP\right)^2=\dfrac{3}{25}.BC^2=300\)
Dấu "=" xảy ra khi \(BP=CP\) hay P là trung điểm BC
P cách B 25m