Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , BC = a , SA = SB = SC = a 3 2 . Tính cosin góc giữa đường thẳng SA và mặt phẳng (ABC).
A. 0
B. 3 2
C. 3 3
D. 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
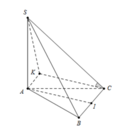
Gọi H là trung điểm của BC thì khi đó SH ⊥ (ABC); suy ra HA là hình chiếu của SA trên (ABC).
Do đó (SA;(ABC)) = (SA;HA) = S H A ^ , mặt khác cos S H A ^ = A H S A = 1 3

Đáp án B
Dựng hình bình hành AKCI khi đó S C ; A I ⏜ = S C ; C K ⏜
Ta có: A B = C K = A B 2 + B C 2 2 = a 6 2
S K = S A 2 + A K 2 = S A 2 + C I 2 = a 6 2
Khi đó cos S C K ⏜ = S C 2 + C K 2 − S K 2 2 S C . C K = 2 3 > 0 Do đó c os S C ; A I ⏜ = 2 3

Đáp án: A.
Hướng dẫn giải: Gọi H là trung điểm của SB
⇒ IH song song với SC.
Do đó SC//(AHI)
![]()
Ta có A I = A B 2 + B I 2 = a 6 2
và I H = S C 2 = S A 2 + A C 2 2 = a
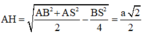
Áp dụng định lý cosin trong tam giác AHI, có
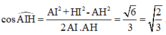

Đáp án B
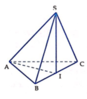
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do S A = S B = S C nên I A = I B = I C ⇒ I là tâm đường tròn ngoại tiếp Δ A B C . Mà Δ A B C vuông cân tại A nên I là trung điểm của BC và I A = I B = I C = 1 2 B C = a 2 2 .
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên S A , A B C ^ = S A , I A ^ = S A I ^ = 45 0 .
Do Δ S I A vuông tại I nên Δ S A I vuông cân tại I, khi đó : S I = I A = a 2 2 ⇒ d S ; A B C = S I = a 2 2

Đáp án B
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của BC.
Ta có ![]()
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của vì thế
![]()
Ta có: ![]()
![]() =
a
2
2
=
a
2
2

Đáp án B
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do SA = SB = SC nên IA = IB = IC => I là tâm đường tròn ngoại tiếp ∆ ABC . Mà ∆ ABC vuông cân tại A nên I là trung điểm của BC và IA = IB = IC = BC/2 = a 2 2
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên
![]()
Do ∆ SIA vuông tại I nên vuông cân tại I, khi đó :
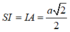
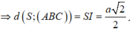

Đáp án B
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của .
Ta có S A , A B C ^ = S A , A M ^ = S A M = 45 0
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của BC vì thế
A M = 1 2 B C = a 2 2
ta có
d S ; A B C = S M = A M . tan S A M = a 2 2 . tan 45 0 = a 2 2
Đáp án C
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.