Cho tập hợp X và các mệnh đề:
(I) X ∪ X = X
(II) X ∩ X = X
(III) X ∩ ∅ = ∅
(IV) ∅ ∪ X = ∅
(V) X \ X = X
(VI) ∅ \ X = ∅
(VII) X \ ∅ = ∅
Trong các mệnh đề trên, có bao nhiêu mệnh đề là đúng?
A. 3
B. 4
C. 5
D. 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Nếu x là một phần tử thuộc tập hợp A thì x ∈ A ; x ⊂ A nên các mệnh đề (I) và (IV) đúng.

Chọn D
Xét hàm số ![]() .
.
Có ![]()
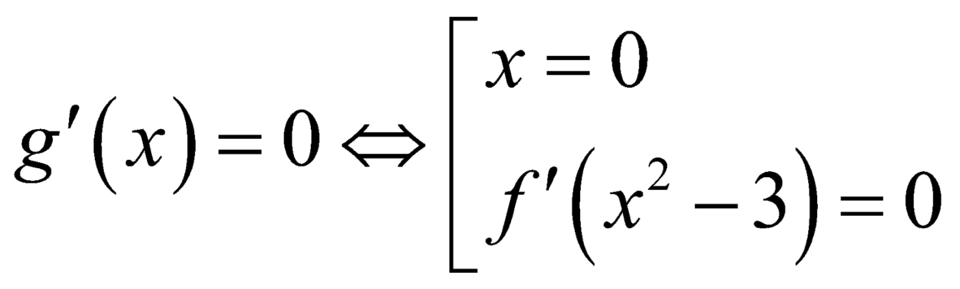
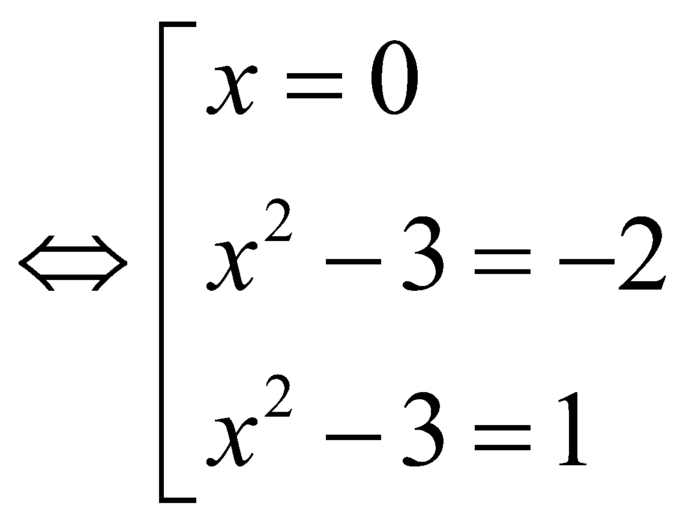
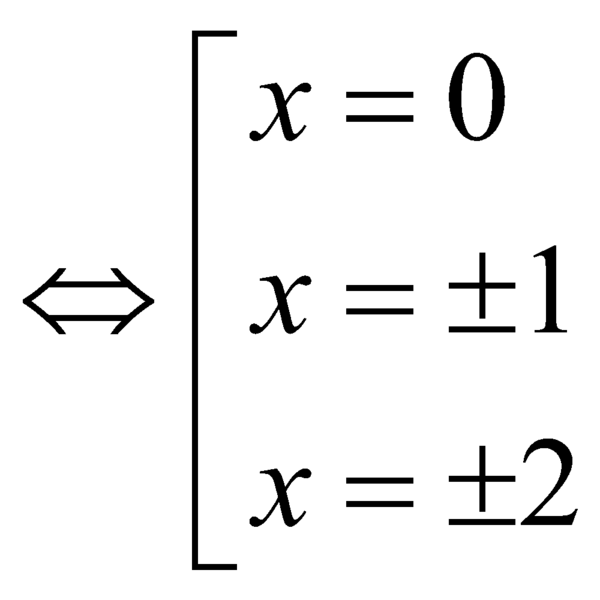 .
.
Ta lại có ![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
![]() thì
thì ![]() . Do đó
. Do đó ![]() thì
thì ![]() .
.
Từ đó ta có bảng biến thiên của ![]() như sau
như sau
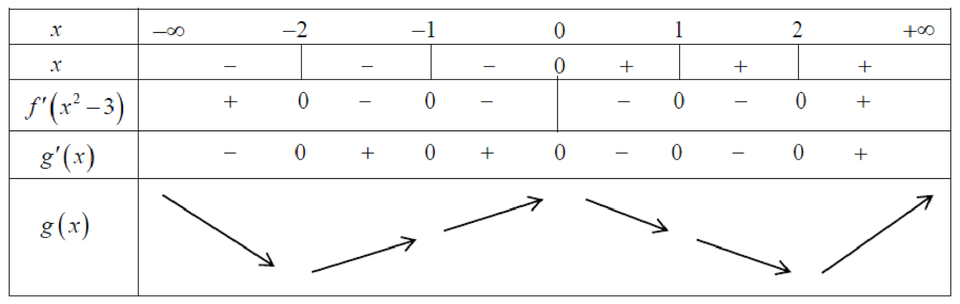
Dựa vào bảng biến thiên, ta có
I. Hàm số ![]() có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
III. Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
IV. Hàm số ![]() đồng biến trên khoảng
đồng biến trên khoảng ![]() LÀ MỆNH ĐỀ ĐÚNG.
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() LÀ MỆNH ĐỀ SAI.
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????

Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I

Chọn A
Đk để hàm số xác định là: ![]() . Vậy mệnh đề
. Vậy mệnh đề ![]() đúng.
đúng.
Do hàm số có tập xác định ![]() nên không tồn tại
nên không tồn tại ![]() do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề
do đó đồ thị hàm số này không có đường tiệm cận ngang. Vậy mệnh đề ![]() sai.
sai.
Do ![]() nên đồ thị hàm số có
nên đồ thị hàm số có ![]() đường tiệm cận đứng là
đường tiệm cận đứng là ![]() và
và ![]() . Vậy
. Vậy ![]() đúng.
đúng.
Ta có
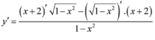
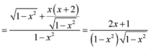
Do ![]() bị đổi dấu qua
bị đổi dấu qua ![]() nên hàm số có một cực trị. Vậy mệnh đề
nên hàm số có một cực trị. Vậy mệnh đề ![]() đúng.
đúng.
Do đó số mệnh đề đúng là ![]() .
.


Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B
Các mệnh đề đúng là: (I), (II), (III), (VI).
Đáp án B