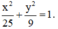Lập phương trình chính tắc của elip trong trường hợp sau: Elip đi qua các điểm M(0; 3) và N(3; -12/5)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 3 2019
Gọi Elip cần tìm có dạng : (E) :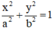 
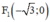là tiêu điểm của (E) ⇒ a2 – b2 = 3 ⇒ a2 = b2 + 3
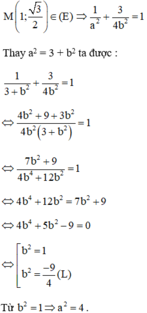
Phương trình chính tắc của Elip là :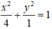 
13 tháng 4 2023
1: (E): x^2/a^2+y^2/b^2=1
Thay x=0 và y=3 vào (E), ta được:
3^2/b^2=1
=>b^2=9
=>b=3
F2(5;0)
=>c=5
=>\(\sqrt{a^2-9}=5\)
=>a^2-9=25
=>a^2=34
=>\(a=\sqrt{34}\)
=>x^2/34+y^2/9=1
2: Thay x=7 và y=0 vào (E), ta được:
7^2/a^2+0^2/b^2=0
=>a^2=49
=>a=7
Thay x=0 và y=3 vào (E), ta được:
0^2/a^2+3^2/b^2=1
=>b^2=9
=>b=3
=>(E): x^2/49+y^2/9=1
3: Thay x=0 và y=1 vào (E), ta được:
1/y^2=1
=>y=1
=>(E): x^2/a^2+y^2/1=1
Thay x=1 và y=căn 3/2 vào (E), ta được:
1^2/a^2+3/4=1
=>1/a^2=1/4
=>a^2=4
=>a=2
=>(E); x^2/4+y^2/1=1
DM
30 tháng 3 2017
Phương trình chính tắc của elip có dạng: +
= 1
a) Elip đi qua M(0; 3):
+
= 1 => b2 = 9
Elip đi qua N( 3; ):
+
= 1 => a2 = 25
Phương trình chính tắc của elip là : +
= 1
b) Ta có: c = √3 => c2 = 3
Elip đi qua điểm M(1; )
+
= 1 =>
+
= 1 (1)
Mặt khác: c2 = a2 – b2
=> 3 = a2 – b2 => a2 = b2 + 3
Thế vào (1) ta được : +
= 1
<=> a2 = 4b2 + 5b2 – 9 = 0 => b2= 1; b2 = ( loại)
Với b2= 1 => a2 = 4
Phương trình chính tắc của elip là : +
= 1.
CM
19 tháng 8 2018
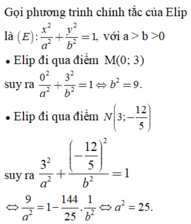
Vậy phương trình cần tìm là E : x 2 25 + y 2 9 = 1.
Đáp án B
20 tháng 5 2017
a) \(\left(E\right):\dfrac{x^2}{100}+\dfrac{y^2}{36}=1\)
b) \(\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\)
CM
3 tháng 11 2019
Đáp án A
Phương trình chính tắc của elip có dạng:
Do Elip đi qua nên:
Lại có :
Như vậy ta có hệ điều kiện:
Giải hệ ta được:
MR
1
Gọi Elip cần tìm có dạng : (E) :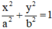
Vậy phương trình chính tắc của elip: