Dựa vào đồ thị hàm số y = cos x, tìm các giá trị của x để cos x = 1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
QD
31 tháng 3 2017
Bài 5. Cosx = .png)
là phương trình xác định hoành độ giao điểm của đường thẳng y = và đồ thị y = cosx.
Từ đồ thị đã biết của hàm số y = cosx, ta suy ra x = .png)
, (k ∈ Z), ( chú ý tìm giao điểm của đường thẳng cới đồ thị trong đoạn [-π ; π] và thấy ngay rằng trong đoạn này chỉ có giao điểm ứng với .png)
rồi sử dụng tính tuần hoàn để suy ra tất cả các giá trị của x là x = , (k ∈ Z)).
SG
1
LT
1 tháng 4 2017
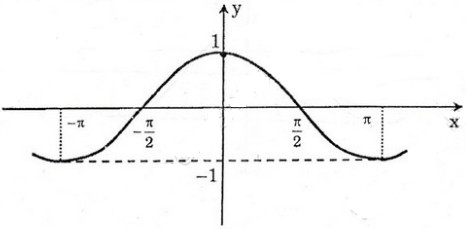
Dựa vào đồ thị hàm số y = cosx, để làm số nhận giá trị âm thì:
KN
2
HP
13 tháng 9 2021
Lí thuyết:
Cho đồ thị \(y=f\left(x\right)\).
\(\Rightarrow\) Vẽ đồ thị \(y=\left|f\left(x\right)\right|\):
- Giữ nguyên phần đồ thị nằm trên trục hoành.
- Lấy đối xứng qua trục hoành phần đồ thị nằm dưới trục hoành.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)
SG
1
LT
1 tháng 4 2017
Nhìn đồ thị y = sinx ta thấy trong đoạn [-π ; π] các điểm nằm phía trên trục hoành của đồ thị y = sinx là các điểm có hoành độ thuộc khoảng (0 ; π). Từ đố, tất cả các khoảng giá trị của x để hàm số đó nhận giá trị dương là (0 + k2π ; π + k2π) hay (k2π ; π + k2π) trong đó k là một số nguyên tùy ý.
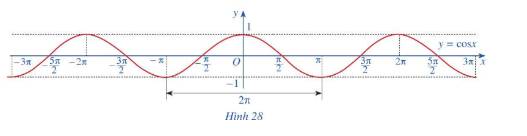
+ Vẽ đồ thị hàm số y = cos x.
+ Vẽ đường thẳng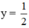
+ Xác định hoành độ các giao điểm.
Ta thấy đường thẳng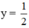
cắt đồ thị hàm số y = cos x tại các điểm có hoành độ