Giải phương trình sau: tan(2x + 1).tan(3x – 1) = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\sqrt 3 \tan 2x = - 1\;\; \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan - \frac{\pi }{6}\; \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \)
\(\;\; \Leftrightarrow x = - \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)
b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { - 5x} \right) \Leftrightarrow 3x = - 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)

a) tan(2x + 1)tan(3x - 1) = 1 ⇔ = 1.
Với điều kiện cos(2x + 1)cos(3x - 1) ≠ 0 phương trình tương đương với
cos(2x + 1)cos(3x - 1) - sin(2x + 1)sin(3x - 1) = 0
⇔ cos(2x + 1 + 3x - 1) = 0 ⇔ 5x = + k π ⇔ x =
+
, k ∈ Z.
Cần chọn các k nguyên để x = +
không thỏa mãn điều kiện của phương trình (để loại bỏ). Điều này chỉ xảy ra trong các trường hợp sau:
(i) x = +
làm cho cos(2x + 1) = 0, tức là
cos[2( +
) + 1] = 0 ⇔
+ 1 =
+ lπ, (l ∈ Z)
⇔ π( -
) = 1 ⇔ π =
, suy ra π ∈ Q, vô lí.
Vì vậy không có k nguyên nào để x = +
làm cho cos(2x + 1) = 0.
(ii) x = +
làm cho cos(3x - 1) = 0. Tương tự (i),ta cũng thấy không có k nguyên nào để x =
+
làm cho cos(3x - 1) = 0.
Vậy ∀ k ∈ Z, x = +
đều là nghiệm của phương trình đã cho.
b)Đặt t = tan x, phương trình trở thành
t + = 1 ⇔ -t2 + 3t = 0 (điều kiện t ≠ 1) ⇔ t = 0 hoặc t = 3 (thỏa mãn)
Vậy tan x = 0 ⇔ x = kπ
tan x = 3 ⇔ x = arctan 3 + kπ (k ∈ Z)

ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{cosx}{sinx}-1=\dfrac{cos^2x-sin^2x}{1+\dfrac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\dfrac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(\dfrac{1}{sinx}-cosx+sinx\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(1-sinx.cosx+sin^2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-sin2x-cos2x\right)=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(3-\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right)=0\)

a. ĐKXĐ: ...
\(\frac{sinx}{cosx}+\frac{sin2x}{cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow\frac{sin2x.cosx+cos2x.sinx}{cosx.cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow\frac{sin3x}{cosx.cos2x}+\frac{sin3x}{cos3x}=0\)
\(\Leftrightarrow sin3x\left(\frac{cosx.cos2x+cos3x}{cosx.cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{cosx\left(2cos^2x-1\right)+4cos^3x-3cosx}{cosx.cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{6cos^2x-4}{cos2x.cos3x}\right)=0\)
\(\Leftrightarrow sin3x\left(\frac{3cos2x-1}{cos2x.cos3x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin3x=0\\cos2x=\frac{1}{3}\end{matrix}\right.\)
b.
\(cos2x\left(2cos^22x-1\right)=\frac{1}{2}\)
\(\Leftrightarrow4cos^32x-2cos2x-1=0\)
Pt bậc 3 này ko giải được, chắc bạn ghi nhầm đề
c. ĐKXĐ: ...
\(\frac{cosx}{sinx}-\frac{sinx}{cosx}=cosx-sinx\)
\(\Leftrightarrow\frac{\left(cosx-sinx\right)\left(cosx+sinx\right)}{sinx.cosx}=cosx-sinx\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\Rightarrow x=...\\\frac{cosx+sinx}{sinx.cosx}=1\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow cosx+sinx=sinx.cosx\)
Đặt \(sinx+cosx=t\Rightarrow\left\{{}\begin{matrix}\left|t\right|\le\sqrt{2}\\sinx.cosx=\frac{t^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow t=\frac{t^2-1}{2}\Rightarrow t^2-2t-1=0\Rightarrow\left[{}\begin{matrix}t=1+\sqrt{2}\left(l\right)\\t=1-\sqrt{2}\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1-\sqrt{2}\Rightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{1-\sqrt{2}}{\sqrt{2}}\Rightarrow x=...\)

a) \(\cos \left( {3x - \frac{\pi }{4}} \right) = - \frac{{\sqrt 2 }}{2}\;\;\;\; \Leftrightarrow \cos \left( {3x - \frac{\pi }{4}} \right) = \cos \frac{{3\pi }}{4}\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x - \frac{\pi }{4} = \frac{{3\pi }}{4} + k2\pi }\\{3x - \frac{\pi }{4} = - \frac{{3\pi }}{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \pi + k2\pi }\\{3x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\)
\( \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + \frac{{k2\pi }}{3}}\\{x = - \frac{\pi }{6} + \frac{{k2\pi }}{3}}\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
b) \(2{\sin ^2}x - 1 + \cos 3x = 0\;\;\;\;\; \Leftrightarrow \cos 2x + \cos 3x = 0\;\; \Leftrightarrow 2\cos \frac{{5x}}{2}\cos \frac{x}{2} = 0\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\cos \frac{{5x}}{2} = 0}\\{\cos \frac{x}{2} = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{{5x}}{2} = \frac{\pi }{2} + k\pi }\\{\frac{{5x}}{2} = - \frac{\pi }{2} + k\pi }\\{\frac{x}{2} = \frac{\pi }{2} + k\pi }\\{\frac{x}{2} = - \frac{\pi }{2} + k\pi }\end{array}} \right.\;\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x = - \frac{\pi }{5} + \frac{{k2\pi }}{5}}\\{x = \pi + k2\pi }\\{x = - \pi + k2\pi }\end{array}} \right.\;\;\;\left( {k \in \mathbb{Z}} \right)\)
c) \(\tan \left( {2x + \frac{\pi }{5}} \right) = \tan \left( {x - \frac{\pi }{6}} \right)\;\; \Leftrightarrow 2x + \frac{\pi }{5} = x - \frac{\pi }{6} + k\pi \;\;\; \Leftrightarrow x = - \frac{{11\pi }}{{30}} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)

Điều kiện: cos 3 x ≠ 0 sin 2 x ≠ 0 ⇔ x ≠ π 6 + k π 3 x ≠ k π 2 k ∈ ℤ .
Phương trình tương đương:
tan 3 x = 1 cot 2 x ⇔ tan 3 x = tan 2 x ⇔ 3 x = 2 x + k π ⇔ x = k π k ∈ ℤ .
Đối chiếu điều kiện, ta thấy nghiệm x = k π không thỏa mãn x ≠ k π 2 .
Vậy phương trình đã cho vô nghiệm.
Chọn đáp án D.

1.
\(\Leftrightarrow3x=k\pi\Leftrightarrow x=\frac{k\pi}{3}\)
2.
\(\Leftrightarrow cos5x=0\Leftrightarrow5x=\frac{\pi}{2}+k\pi\Leftrightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
4.
\(cos3x+cosx+cos2x=0\)
\(\Leftrightarrow2cos2x.cosx+cos2x=0\)
\(\Leftrightarrow cos2x\left(2cosx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cosx=-\frac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+\frac{k\pi}{2}\\x=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
5.
\(sin6x+sin2x+sin4x=0\)
\(\Leftrightarrow2sin4x.cos2x+sin4x=0\)
\(\Leftrightarrow sin4x\left(2cos2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=0\\cos2x=-\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{4}\\x=\pm\frac{\pi}{3}+k\pi\end{matrix}\right.\)
6. ĐKXĐ; ...
\(\Leftrightarrow tanx+tan2x=1-tanx.tan2x\)
\(\Leftrightarrow\frac{tanx+tan2x}{1-tanx.tan2x}=1\)
\(\Leftrightarrow tan3x=1\)
\(\Leftrightarrow x=\frac{\pi}{12}+\frac{k\pi}{3}\)
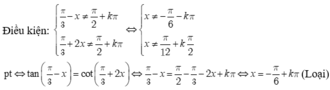
Điều kiện: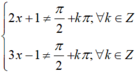
Vậy phương trình có họ nghiệm