Trong không gian với hệ tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng d : x - 2 2 = y - 3 3 = z + 4 - 5 và d ' : x + 1 3 = y - 4 - 2 = z - 4 - 1
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi d là đường thẳng cần tìm

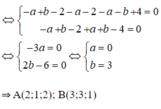
d đi qua điểm A(2;1;2) và có vectơ chỉ phương ![]()


Đáp án C
Gọi B 2 + t ; - 1 - t ; 1 + t A B ¯ = 1 + t ; - t ; t - 2 . Cho A B ¯ . u d ¯ = 0 ⇔ t + 1 - 4 t - 2 t + 4 = 0 ⇔ t = 1 ⇒ A B ¯ = 2 ; - 1 ; - 1
Khi đó d : x - 1 2 = y + 1 - 1 = z - 3 - 1 .

Chọn đáp án A
Đường thẳng d 1 , d 2 lần lượt có vecto chỉ phương là u 1 ⇀ = 1 ; 1 ; - 1 và u 2 ⇀ = 2 ; 1 ; 2
Gọi ∆ là đường thẳng cần tìm và có vecto chỉ phương là u ∆ ⇀ , khi đó A ∈ ∆ và ∆ ⊥ d 1 , ∆ ⊥ d 2
Suy ra
![]()
Loại ngay C và D (vì hai đường thẳng ở hai phương án này có vecto chỉ phương không cùng phương với u ∆ ⇀ ).
Xét A: Ta thấy
![]()
nên đường thẳng![]() đi qua điểm A(1;2;1)
đi qua điểm A(1;2;1)
Xét B: Ta thấy
![]()
nên đường thẳng ![]() không đi qua điểm A(1;2;1)
không đi qua điểm A(1;2;1)

Chọn C
Vectơ chỉ phương của d1 và d2 lần lượt là ![]()
Gọi AB là đoạn vuông góc chung của d1 và d2 với A ∈ d1 và B ∈ d2
Suy ra: A (-1+2a; -1+a; -1+3a); B (2+b; 2b; 9+3b)
Khi đó: ![]() = (-2a + b + 3; -a + 2b + 1; -3a + 3b + 10) Vì là đoạn vuông góc chung của d1 và d2 nên:
= (-2a + b + 3; -a + 2b + 1; -3a + 3b + 10) Vì là đoạn vuông góc chung của d1 và d2 nên:

Gọi I là tâm mặt cầu (S) có đường kính là AB.
Suy ra 
Vậy phương trình mặt cầu:

Chọn A
Ta có M ∈ d suy ra M (2 + 2m; 3 + 3m; -4 -5m)
Tương tự N ∈ d’ suy ra N (-1 + 3n; 4 – 2n; 4 – n)
Từ đó ta có
Mà do MN là đường vuông góc chung của d và d’ nên:
Suy ra M (0;0;1), N (2;2;3).