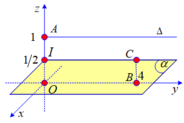
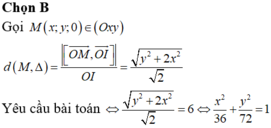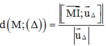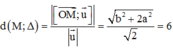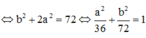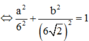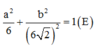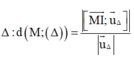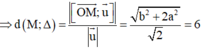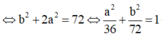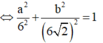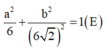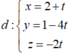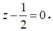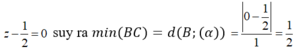Trong không gian với hệ tọa độ Oxyz, cho đường thẳng Δ đi qua gốc tọa độ O và điểm I (0; 1; 1). Gọi S là tập hợp các điểm nằm trên mặt phẳng (Oxy), cách đường thẳng Δ một khoảng bằng 6. Tính diện tích hình phẳng giới hạn bởi S.
A. 36π
B.
36
2
π
C. 18 2 π
D. 18π