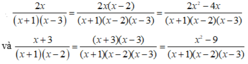Biến đổi và với và thành cặp phân thức bằng nó và có cùng mẫu thức.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

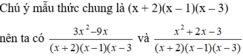

\(\dfrac{x^2-1}{\left(x+1\right)\left(x-3\right)}\)
\(=\dfrac{x^2-1^2}{\left(x+1\right)\left(x-3\right)}\)
\(=\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)\left(x-3\right)}\)
\(=\dfrac{x-1}{x-3}\)
Vậy đã biến đổi phân thức đó thành một phân thức bằng nó và có tử bằng với đa thức \(A=x-1\)

b. Tự đặt đk
\(x^{^2}+5\sqrt{x-3}=21\\\Leftrightarrow x^{^2}-9+5\sqrt{x-3}=12 \)
Đặt \(a=\sqrt{x-3}\) \(\left(a\ge0\right)\) Phương trình trở thành:
\(a^{^2}\left(a^{^2}+6\right)+5a=12\\ \Leftrightarrow a^{^4}+6a^{^2}+5a-12=0\\ \Leftrightarrow a^{^4}-a^{^3}+a^{^3}-a^{^2}+7a^{^2}-7a+12a-12=0\\ \Leftrightarrow\left(a-1\right)\left(a^{^3}+a^{^2}+7a+12\right)=0\\ \Leftrightarrow a=1\left(tmdk\right)\)
Ta có: vì \(a\ge0\) nên \(a^{^3}+a^{^2}+7a+12\ne0\)
Với a = 1 ta có x=4 (tmdk)

a) Ta có x + y = 25
=> (x + y)2 = 625
=> x2 + y2 + 2xy = 625
=> x2 + y2 + 10 = 625
=> x2 +y2 = 615
b) Ta có x + y = 3
=> (x + y)3 = 27
=> x3 + 3x2y + 3xy2 + y3 = 27
=> x3 + y3 + 3xy(x + y) = 27
=> x3 + y3 + 9xy = 27
Lại có x + y = 3
=> (x + y)2 = 9
=> x2 + y2 + 2xy = 9
=> 2xy = 4
=> xy = 2
Khi đó x3 + y3 + 9xy + 27
=> x3 + y3 + 18 = 27
=> x3 + y3 = 9
c) Ta có x - y = 5
=> (x - y)2 = 25
=> x2 + y2 - 2xy = 25
=> 2xy = -10
=> xy = -5
Khi đó : x3 - y3 = (x - y)(x2 + xy + y2) = 5(15 - 5) = 5.10 = 50
Bài 4.
a) x2 + y2 = x2 + 2xy + y2 - 2xy
= ( x2 + 2xy + y2 ) - 2xy
= ( x + y )2 - 2xy
= 252 - 2.136
= 625 - 272
= 353
b) x + y = 3
⇔ ( x + y )2 = 9
⇔ x2 + 2xy + y2 = 9
⇔ 5 + 2xy = 9 ( gt x2 + y2 = 5 )
⇔ 2xy = 4
⇔ xy = 2
x3 + y3 = x3 + 3x2y + 3xy2 + y3 - 3x2y - 3xy2
= ( x3 + 3x2y + 3xy2 + y3 ) - ( 3x2y + 3xy2 )
= ( x + y )3 - 3xy( x + y )
= 33 - 3.2.3
= 27 - 18
= 9

\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+x\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^3+x^2+2x^2+2x\right)\left(x+3\right)+1\)
\(=\left(x^3+3x^2+2x\right)\left(x+3\right)+1\)
\(=x^4+3x^3+2x^2+3x^3+9x^2+6x+1\)
\(=x^4+\left(3x^3+3x^3\right)+\left(2x^2+9x^2\right)+6x+1\)
\(=x^4+6x^3+11x^2+6x+1\)
\(=\left(x^2+3x+1\right)^2\) (Bằng vế phải)
\(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left[x\left(x+3\right)\right]\left[\left(x+1\right)\left(x+2\right)\right]+1\)
\(=\left(x^2+3x\right)\left(x^2+2x+x+2\right)+1\)
\(=\left(x^2+3x+1-1\right)\left(x^2+3x+1+1\right)+1\)
\(=\left(x^2+3x+1\right)^2-1^2+1\)
\(=\left(x^2+3x+x\right)^2\)

a) ĐK: \(x\ge3\)
PT \(\Leftrightarrow\sqrt{\left(x-3\right)\left(x-2\right)}-\sqrt{x-2}+\sqrt{x+1}-\sqrt{\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x-3}-1\right)+\sqrt{x+1}\left(1-\sqrt{x-3}\right)=0\)
\(\Leftrightarrow\left(\sqrt{x-2}-\sqrt{x+1}\right)\left(\sqrt{x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-2}=\sqrt{x+1}\\\sqrt{x-3}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x-2=x+1\\x-3=1\end{matrix}\right.\) \(\Leftrightarrow x=4\) (Thỏa mãn)
Vậy ...