Tìm tất cả các giá trị thực của m để phương trình log2( -x2 - 3x – m + 10) = 3 có nghiệm thực phân biệt trái dấu.
A. m < 4
B. m > 2
C. m < 2
D. m > 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Đặt ![]()
Khi đó, phương trình f(
4
x
-
x
2
) =
log
2
m
trở thành ![]()
Để phương trình f( 4 x - x 2 ) = log 2 m có 4 nghiệm thực phân biệt thì đường thẳng y = log 2 m cắt đồ thị hàm số y = f(t) tại hai điểm phân biệt thỏa mãn t < 4.
Suy ra ![]()
Vậy m ∈ ( 1 2 ;8).

Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)

Chọn C.
Phương pháp: Biến đổi đưa về phương trình tích.
Cách giải:
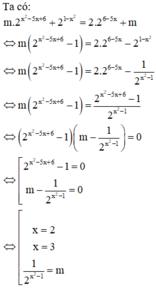
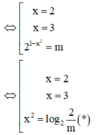
Vậy để phương trình đã cho có 4 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt khác 2 và 3.
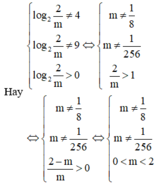
Chọn C.