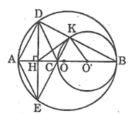
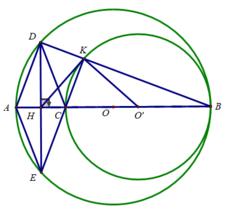
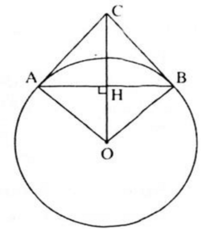
Cho AB là đường kính của đường tròn (O;R). C là một điểm thay đổi trên đường tròn ( C khác A và B), kẻ CH vuông góc với AB tại H .Gọi I là trung điểm của AC, OI cắt tiếp tuyến tại A của đường tròn (O;R) tại M, MB cắt CH tại K.
a) Chứng minh 4 điểm C,H,O,I cùng thuộc một đường tròn
b) Chứng minh MC là tiếp tuyến của (O;R)
c) Chứng minh K là trung điểm của CH
d) Xác định vị trí của C để chu vi tam giác ACB đạt giá trị lớn nhất? Tìm giá trị lớn nhất đó theo R
đang cần gấp mn giải lẹ giùm mình