Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
1.
\(V=\pi\int\limits^1_0x^6dx=\dfrac{\pi x^7}{7}|^1_0=\dfrac{\pi}{7}\)
2.
\(F\left(x\right)=\int sin2xdx=-\dfrac{1}{2}cos2x+C\)
\(f\left(\dfrac{\pi}{4}\right)=1\Leftrightarrow-\dfrac{1}{2}cos\dfrac{\pi}{2}+C=1\Rightarrow C=1\)
\(\Rightarrow F\left(x\right)=-\dfrac{1}{2}cos2x+1\Rightarrow F\left(\dfrac{\pi}{6}\right)=\dfrac{3}{4}\)
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
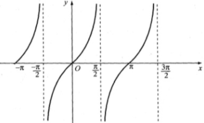
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
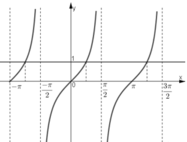
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
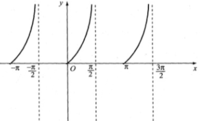
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
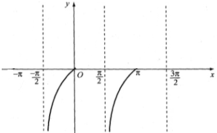
Chọn A