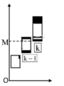
Người ta thực hiện giao thoa ánh sáng bằng ánh sáng trắng, dùng kính lọc sắc để chỉ cho ánh sáng từ màu tím đến màu vàng đi qua hai khe (có bước sóng từ 0,38 µm đến 0,6 µm). Biết khoảng cách giữa 2 khe là a = 1 mm, khoảng cách từ 2 khe đến màn là D = 2 m. Khoảng cách bề rộng nhỏ nhất mà không có vân sáng nào quan sát được ở trên màn là
A. 0,75 mm
B. 0,32 mm
C. 1 mm
D. 0,5 mm.

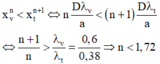
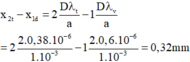

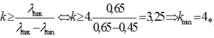

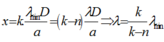


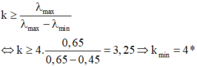
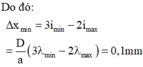
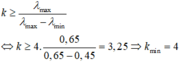
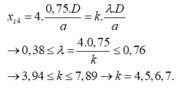


Đáp án B
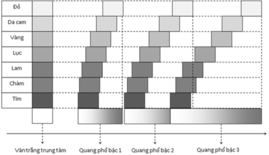
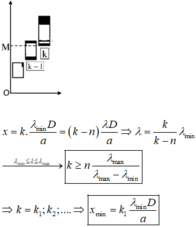
Với hiện tượng giao thoa nhiều ánh sáng đơn sắc, khi bậc quang phổ càng cao thì các quang phổ thường chồng khít lên nhau do vậy ta chỉ có thể tìm thấy vị trí vân tối ở gần vân sáng trung tâm
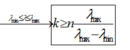
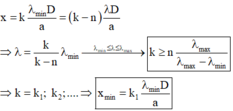
+ Cụ thể ta xét quang phổ bậc n của phổ bậc n + 1, để hai hệ quang phổ này không chồng lên nhau thì vị trí vân sáng bậc n của ánh sáng vàng phải nhỏ hơn vị trí vân sáng bậc n + 1 của ánh sáng tím
→ n < 1 , 72
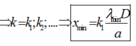
Vậy để có thể tìm thấy vâng tối thì n = 1
Khoảng cách đó là