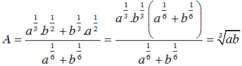Đơn giản biểu thức: A = a 1 3 b + b 1 3 a a 6 + b 6 ( a ; b > 0 ) ta được:
A. A = ab
B. A = ab 3
C. A = ab 6
D. A = a 6 - b 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(152-\left(374+152\right)+\left(-65+374\right)\)
= \(152-374-152-65+374\)
= \(\left(152-152\right)+\left(374-374\right)-65=-65\)
b)
13 - 12 + 11 + 10 - 9 + 8 - 7 - 6 -5 - 4 - 3 - 2 - 1
= \(-7+\left(13+11+10+8\right)-\left(1+2+3+4+5+6+9+12\right)\)
= \(-7+42-42\)
= -7
2)
\(-\left(a-b-c\right)+\left(-c+b+a\right)-\left(a+b\right)\)
= \(-a+b+c-c+b+a-a-b\)
= \(\left(-a+a-a\right)+\left(b+b-b\right)+\left(c-c\right)\)
= -a + b
= b - a

Bài 2
P=a-(\(\frac{1}{\sqrt{a}-\sqrt{a-1}}-\frac{1}{\sqrt{a}+\sqrt{a-1}}\)
P=a-(\(\frac{\sqrt{a}+\sqrt{a-1}}{a-a+1}-\frac{\sqrt{a}-\sqrt{a-1}}{a-a+1}\)
P=a-\(2\sqrt{a-1}\)
P=a-1-2\(\sqrt{a-1}+1\)
P=\(\left(\sqrt{a-1}-1\right)^2\)
Có \(\left(\sqrt{a-1}-1\right)^2>=0vớimọix\)
=> P >=0

a)
\(A=\dfrac{a^{\dfrac{4}{3}}\left(a^{-\dfrac{1}{3}}+a^{\dfrac{2}{3}}\right)}{a^{\dfrac{1}{4}}\left(a^{\dfrac{3}{4}}+a^{-\dfrac{1}{4}}\right)}=\dfrac{a^{\left(\dfrac{4}{3}-\dfrac{1}{3}\right)+}a^{\left(\dfrac{4}{3}+\dfrac{2}{3}\right)}}{a^{\left(\dfrac{1}{4}+\dfrac{3}{4}\right)}+a^{\left(\dfrac{1}{4}-\dfrac{1}{4}\right)}}=\dfrac{a+a^2}{a+1}=\dfrac{a\left(a+1\right)}{a+1}\)
\(a>0\Rightarrow a+1\ne0\) \(\Rightarrow A=a\)

bài này mình cũng dò lại đề rồi mình chép đúng đấy mà không làm được nên mới nhờ giải

\(M=\frac{\left(a^{\frac{1}{3}}+b^{\frac{1}{3}}\right)^2}{\sqrt[3]{ab}}:\left(2+\sqrt[3]{\frac{a}{b}}+\sqrt[3]{\frac{b}{a}}\right)=\frac{\left(a^{\frac{1}{3}}+b^{\frac{1}{3}}\right)^2}{\sqrt[3]{ab}}:\frac{2\sqrt[3]{ab}+\left(\sqrt[3]{a}\right)^2+\left(\sqrt[3]{a}\right)^2}{\sqrt[3]{ab}}\)
\(=\frac{\left(\sqrt[3]{a}+\sqrt[3]{b}\right)^2}{\sqrt[3]{ab}}-\frac{\sqrt[3]{ab}}{\left(\sqrt[3]{a}+\sqrt[3]{b}\right)^2}=1\)

Bài 1:
\(a,\left(a+b-c\right)-\left(b-c-d\right)\)
\(=a+b-c-b+c+d\)
\(=a+d\)
\(b,-\left(a-b+c\right)+\left(a-b+d\right)\)
\(=-a+b-c+a-b+d\)
\(=-c+d\)
\(c,\left(a+b\right)-\left(-a+b-c\right)\)
\(=a+b+a-b+c\)
\(=2a+c\)
\(d,-\left(a+b\right)+\left(a+b+c\right)\)
\(=-a-b+a+b+c\)
\(=c\)
Bài 3 :
\(a,15-\left(4-x\right)=6\)
\(4-x=15-6\)
\(4-x=9\)
\(x=4-9\)
\(x=-5\)
\(b,-30+\left(25-x\right)=-1\)
\(25-x=-1+30\)
\(25-x=29\)
\(x=25-29\)
\(x=-4\)
\(c,x-5=-1\)
\(x=-1+5\)
\(x=4\)
\(d,x-4=-10\)
\(x=-10+4\)
\(x=-6\)
\(e,x+3=-8\)
\(x=-8-3\)
\(x=-11\)
\(g,x+6=0\)
\(x=-6\)
Câu 1:
A, (a+b-c)-(b-c-d)
= a+b-c-b+c+d
= a+(b-b)+(c-c)
= a
B, -(a-b+c)+(a-b+d)
= -a+b-c+a+b+d
= (a-a)+(b+b)+d-c
= 2b+d-c
C, (a+b)-(-a+b-c)
= a+b+a-b+c
= (a+a)+(b-b)+c
= 2a+c
D, -(a+b)+(a+b+c)
= -a-b+a+b+c
= (-a+a)+(b-b)+c
= c
=

Bài 4: Đơn giản các biểu thức sau khi bỏ dấu ngoặc
a/ (a + b - c) - (b - c + d)
= a + b - c - b +c - d
= a + (b - b) + (-c + c) - d
= a - d
b/ -(a-b+c)+(a-b+d)
= -a + b - c + a - b + d
= (-a + a) + (b - b) - c + d
= -c + d
c/ (a+b)-(-a+b-c)
= a + b + a - b + c
= 2a + c
d/ -(a+b) + (a+b+c)
= -a - b + a + b + c
= c
Chọn A.
Ta có: