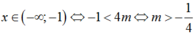Với giá trị nào của m thì biểu thức T = 34 + ln( 4m - x) xác định với mọi x ∈ - ∞ ; - 1 ?
A. m > -4
B. m > -1/4
C. m < -4
D. m < -1/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 8 2017
Chọn C.
Biểu thức f(x) xác định khi x - m > 0 hay x > m.
Để f(x) xác định với mọi 
thì m ≤ - 3.
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2020
\(\Leftrightarrow\left(2m-1\right)sinx-\left(m+2\right)cosx+4m-3\ge0\) ;\(\forall x\)
\(\Leftrightarrow m\ge\dfrac{sinx+2cosx+3}{2sinx-cosx+4}=P\)
\(\Leftrightarrow m\ge P_{max}\)
Ta có: \(P=\dfrac{sinx+2cosx+3}{2sinx-cosx+4}\Leftrightarrow\left(2P-1\right)sinx-\left(P+2\right)cosx=3-4P\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(3-4P\right)^2\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Rightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow m\ge2\)
6 tháng 3 2021
a) ĐKXĐ: \(x\notin\left\{-3;2\right\}\)
b) Ta có: \(P=\dfrac{x^3+2x^2-5x-6}{x^2+x-6}\)
\(=\dfrac{x^3+3x^2-x^2-3x-2x-6}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2\left(x+3\right)-x\left(x+3\right)-2\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x+3\right)\left(x^2-x-2\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+1\right)}{x-2}=x+1\)
Với mọi x nguyên thỏa ĐKXĐ, ta luôn có: x+1 là số nguyên
hay P là số nguyên(đpcm)
Chọn B.
Biểu thức T xác định khi và chỉ khi 4m – x > 0 hay x < 4m.
Để T xác định với mọi