Cho biết tổng S = x + x 2 + x 3 + . . . + x n . Tìm điều kiện của x để lim n → + ∞ S = x 1 - x
A. x < 1
B. x ≠ 0
C. x > 0
D. x ≠ 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 56 ⋮ 8
32 ⋮ 8
8 ⋮ 8
Để S ⋮ 8 thì x ⋮ 8
Vậy x = 8k (k ∈ ℕ)
b) 56 ⋮ 4
32 ⋮ 4
8 ⋮ 4
Để S không chia hết cho 4 thì x không chia hết cho 4
Vậy x ≠ 4k (k ∈ ℕ)

Chọn A.
- Ta có, S là tổng của n số hạng của một cấp số nhân với 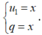
- Suy ra 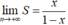 khi đó là cấp số nhân lùi vô hạn.
khi đó là cấp số nhân lùi vô hạn.
- Do đó |q| < 1 hay |x| < 1.

S = 88 - 8 + x
S = 80 + x
như vậy là S \(⋮\)8
vì 80 \(⋮\)8 nên ta có x = {x E N* | x \(⋮\)8}
Cho tổng S = 56 + 32 - 8 + x với x thuộc N. Tìm điều kiện của x sao cho S không chia hết cho 4

S = 56 + 32 - 16 + x
S = 88 - 16 + x
S = 72 + x
Để S chia hết cho 8 thì 72 và x phải chia hết cho 8
Mà 72 chia hết cho 8
=> x chia hết cho 8

Để A la phan so thi x-1 phải khác 0
Hay x phai khac 1
Neu x bang 2 ta dc 2/2-1=2/1=2
Neu x bang (-3) thi ta dc 2/(-3)-1=2/-4=-1/2
c) de A co gia tr la so nguyen thi x-1 Thuộc Ư (2)=(-1);1(-2);2
Neu x-1=(-1)thi x =(-1)+1=0
Neu x -1 =1 thi x=1+1=2
Neu x-1=2 thi x=2+1=3
Neu x-1=(-2) thi x=(-2)+1=-1
Vay x bang 0;2;3;(-1)
k cho minh nha

Ta có: \(x+y=m+n\Rightarrow n=x+y-m\)
\(\Rightarrow S=x^2+y^2+m^2+\left(x+y-m\right)^2\)
\(=x^2+y^2+m^2+(x^2+y^2+m^2+2xy-2mx-2my)\)
\(=x^2+y^2+m^2+(x^2+y^2+m^2+2xy-2mx-2my)\)
\(=x^2+y^2+m^2+x^2+y^2+m^2+2xy-2mx-2my\)
\(=\left(x^2+2xy+y^2\right)+\left(m^2-2mx+x^2\right)+\left(m^2-2my+y^2\right)\)
\(=\left(x+y\right)^2+\left(m-x\right)^2+\left(m-y\right)^2\)
Vì x, y, m, n \(\in\) Z nên x + y; m - x; m - y là số nguyên
Vậy S luôn bằng tổng các bình phương của 3 số nguyên

S=5+120+x(x thuộc N)=125+x
a)Để S chia hết cho 5 thì 125+x chia hết cho 5 hay 125+x thuộc B(5)={0;5;10;...}
mà x thuộc N nên x thuộc{0;5;...}
b)Để S không chia hết cho 5 thì x khác{0;5;10;15;...} (hay các số có tận cùng là 0 hoặc 5)
c)Để S chia hết cho 10 thì x thuộc{5;15;25;...} (các số có tận cùng là 5)
Chọn A.
- Ta có, S là tổng của n số hạng của một cấp số nhân với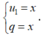
- Suy ra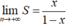 khi đó là cấp số nhân lùi vô hạn.
khi đó là cấp số nhân lùi vô hạn.
- Do đó |q| < 1 hay |x| < 1.