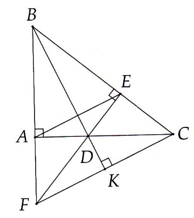
cho tam giác ABC vuông tại A một đường thẳng cắt 2 cạnh AB , AC ở D và E , CM : CD2 - CB2 = ED2 - EB2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng định lý Pitago cho tam giác vuông ACD:
\(CD^2=AD^2+AC^2\)
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(CB^2=AB^2+AC^2\)
\(\Rightarrow CD^2-CB^2=AD^2+AC^2-AB^2-AC^2=AD^2-AB^2\) (1)
Áp dụng định lý Pitago cho tam giác vuông ADE:
\(ED^2=AD^2+AE^2\)
Áp dụng định lý Pitago cho tam giác vuông ABE:
\(EB^2=AB^2+AE^2\)
\(\Rightarrow ED^2-EB^2=AD^2+AE^2-AB^2-AE^2=AD^2-AB^2\) (2)
(1);(2) \(\Rightarrow CD^2-CB^2=ED^2-EB^2\)
Ta cần CM: \(CD^2-CB^2=ED^2-EB^2\Leftrightarrow CD^2-AB^2-AC^2=ED^2-EB^2\Leftrightarrow EB^2-AB^2=ED^2-\left(CD^2-AC^2\right)\Leftrightarrow AE^2=ED^2-AD^2\left(luônđúng\right)\) (vì các tam giác ACD, ABE,ADE đều vuông tại A) \(\Rightarrowđpcm\)

a: AB=8cm
b: xét ΔABE vuông tại A và ΔDBE vuông tại D có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE