Trong mặt phẳng tọa độ Oxyz, tập hợp điểm biểu diễn của các số phức z=2+bi với bÎR là đường thẳng
A. x = 2
B. Song song với trục Ox
C. y = 2
D. Vuông góc với trục Oy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Vì A, B, C lần lượt là hình chiếu vuông góc của M trên trục Ox, Oy, Oz nên: A − 3 ; 0 ; 0 B 0 ; 2 ; 0 C 0 ; 0 ; 4

Em có M’ là hình chiếu song song của M trên (ABC)
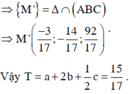

Đáp án D
Vì A, B, C lần lượt là hình chiếu vuông góc của M trên trục Ox, Oy, Oz nên: A − 3 ; 0 ; 0 B 0 ; 2 ; 0 C 0 ; 0 ; 4

Em có M’ là hình chiếu song song của M trên (ABC)
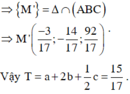

Gọi A(a;0;0), B(0;b;0) ![]()
Vì ![]()
![]()
Khi đó
![]()
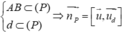 =(-1;-2;-5)
=(-1;-2;-5)
Và (P) đi qua điểm
![]()
Chọn đáp án C.

Đáp án C
Ta có n α → = u O y → , u d → = - 4 ; 0 ; 2 ⇒ α : 2 x - z = 0

Chọn C
Cách 1:
Đường thẳng d qua điểm M(1;-2;0), có véc tơ chỉ phương a → = ( 1 ; - 1 ; - 2 ) và trục Oy có véc tơ chỉ phương j → = ( 0 ; 1 ; 0 ) .
![]()
là một véc tơ pháp tuyến của mặt phẳng (P).
![]()
![]()
![]()
Gọi φ là góc giữa mặt phẳng (P) và trục Oy 0 ≤ φ ≤ π 2
Ta có
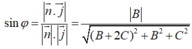
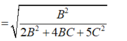
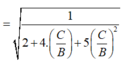
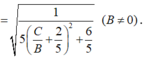
Vì hàm số sin φ tăng liên tục trên 0 ; π 2 nên φ đạt giá trị lớn nhất khi sin φ lớn nhất
Lúc đó
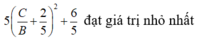

Chọn B= 5; C=-2, A = 1 => n → = ( 1 ; 5 ; - 2 )
Phương trình mặt phẳng (P) qua điểm M, có véc tơ pháp tuyến n → = ( 1 ; 5 ; - 2 ) là:
![]()
![]()
Thế tọa độ N(-1;-2;-1) vào phương trình mặt phẳng (P): -1+5(-2)-2(-1)+9=0 (luôn đúng).
Vậy điểm N(-1;-2;-1) thuộc mặt phẳng (P).
Cách 2:
Xét bài toán tổng quát: Cho hai đường thẳng ∆ 1 , ∆ 2 phân biệt và không song song với nhau. Viết phương trình mặt phẳng (P) chứa đường thẳng ∆ 1 và tạo với ∆ 2 một góc lớn nhất.
Phương pháp giải:
+) Vẽ một đường thẳng ∆ 3 bất kỳ song song với ∆ 2 và cắt ∆ 1 tại M. Gọi B là điểm cố định trên ∆ 3 và H là hình chiếu vuông góc của B lên mp (P), kẻ BA ⊥ ∆ 1

![]()
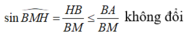
![]()
![]()
và (P) chứa ∆ 1 và vuông góc với mặt phẳng ( ∆ 1 , ∆ 2 )
Vậy (P) có VTPT là
![]()
Áp dụng:
![]()
![]()
Phương trình mặt phẳng (P) qua điểm M(1;-2;0), có véc tơ pháp tuyến là
![]()
Vậy điểm N(-1;-2;-1) thuộc mặt phẳng (P).
Chọn A