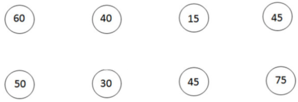
Nối hai số có tổng bằng 90:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
30 tháng 3 2021
Kết luận nào sau đây đúng ?
A. Hai góc kề nhau có tổng số đo bằng 90 độ
B. Hai góc phụ nhau có tổng số đo bằng 180 độ
C. Hai góc bù nhau có tổng số đo bằng 90 độ
D. Hai góc bù nhau có tổng số đo bằng 180 độ
10 tháng 9 2018
Lấy P và Q lần lượt là trung điểm của OB và OC.
Xét \(\Delta\)BOC có: D là trung điểm của BC; P là trung điểm của OB => DP là đường trung bình \(\Delta\)BOC
=> DP // OC và DP = 1/2.OC. Mà Q là trung điểm OC => DP // OQ và DP = OQ
Xét tứ giác DPOQ có: DP // OQ; DP = OQ => Tứ giác DPOQ là hình bình hành
=> ^DPO = ^DQO (1)
Xét \(\Delta\)BHO: ^OHB = 900; P là trung điểm OB => HP = OP = BP
Lại có: Tứ giác DPOQ là hbh (cmt) => OP = DQ => HP = DQ
Tương tự ta cũng có: DP = KQ
Mặt khác: HP = BP (cmt) => \(\Delta\)BHP cân tại P
Xét \(\Delta\)BHP cân đỉnh P có góc ngoài là ^HPO => ^HPO = 2.^HBP = 2.^ABO (2)
Tương tự: ^KQO = 2.^ACO (3)
Từ (2) và (3) kết hợp với ^ABO = ^ACO (gt) => ^HPO = ^KQO (4)
Từ (1) và (4) suy ra ^DPO + ^HPO = ^DQO + ^KQO => ^HPD = ^DQK
Xét \(\Delta\)PHD và \(\Delta\)QDK có: DP = KQ; HP = DQ; ^HPD = ^DQK => \(\Delta\)HPD = \(\Delta\)QDK (c.g.c)
=> HD = DK (2 cạnh tương ứng) => \(\Delta\)HDK cân ở D
Xét \(\Delta\)HDK cân đỉnh D có M là trung điểm cạnh HK => DM vuông góc HK (đpcm).
CM
14 tháng 6 2018
Phương pháp giải:
Chọn và nối các số có tổng là 100.
Lời giải chi tiết:
29 tháng 12 2015
gọi hai số là a là số thứ nhất & b là số thứ 2. ta có: a + b = 90 --> a = 90 - b
Nếu số thứ nhất giảm đi 10% = 0,1 --> còn lại 0,9a
số thứ 2 giảm đi 20% = 0,2 --> còn lại 0,8b, khi đó ta có tổng mới: 0,9a + 0,8b = 76
<=> 9a + 8b = 760 mà a = 90 -b --> 9(90-b) + 8b = 760
<=> 810 - 9b + 8b = 760
--> b = 810 - 760 = 50
a = 90 - 50 = 40
Phương pháp giải:
- Tìm hai trong các số đã cho mà khi cộng lại thì được kết bẳng 90.
- Nối hai số đó.
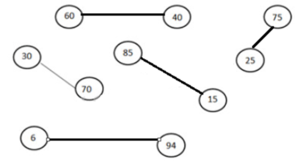
Lời giải chi tiết: