Tọa độ các giao điểm của đồ thị hàm số y = - 3 x + 1 với các trục Ox, Oy lần lượt là:
A. 1 ; - 2 v à 0 ; 1
B. 1 3 ; 0 v à 0 ; 1
C. - 1 ; 4 v à 1 3 ; 0
D. 0 ; 1 v à 1 ; 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2
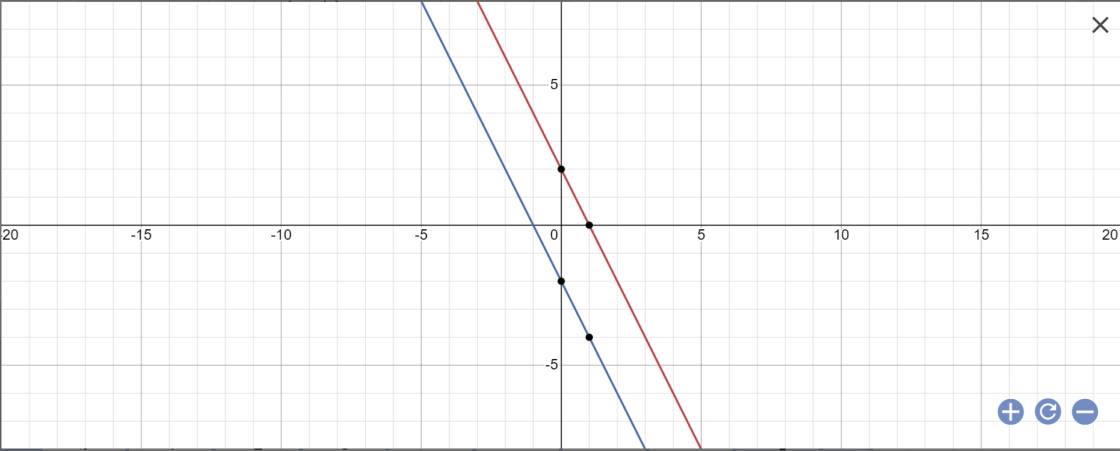

b. Đồ thị đt đề cho là y=6
PTGD 2 đt đầu bài với đt câu b là: \(\left\{{}\begin{matrix}2x=6\\x-1=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\rightarrow A\left(3;6\right)\\x=7\rightarrow B\left(7;6\right)\end{matrix}\right.\)

1: Bạn bổ sung đề bài đi bạn
2: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\left(2m-1\right)x=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{4}{2m-1}\\y=0\end{matrix}\right.\)
=>\(OA=\sqrt{\left(\dfrac{4}{2m-1}-0\right)^2+\left(0-0\right)^2}=\dfrac{4}{\left|2m-1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\left(2m-1\right)\cdot0-4=-4\end{matrix}\right.\)
=>OB=4
Để ΔOAB cân tại O thì OA=OB
=>\(\dfrac{4}{\left|2m-1\right|}=4\)
=>\(\dfrac{1}{\left|2m-1\right|}=1\)
=>\(\left|2m-1\right|=1\)
=>\(\left[{}\begin{matrix}2m-1=1\\2m-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=2\\2m=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=0\end{matrix}\right.\)

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+2014≥2014
Hơn nữa A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=412x−1=0 \Leftrightarrow x=\dfrac{1}{4}⇔x=41 .
Vậy GTNN = 2014

a: 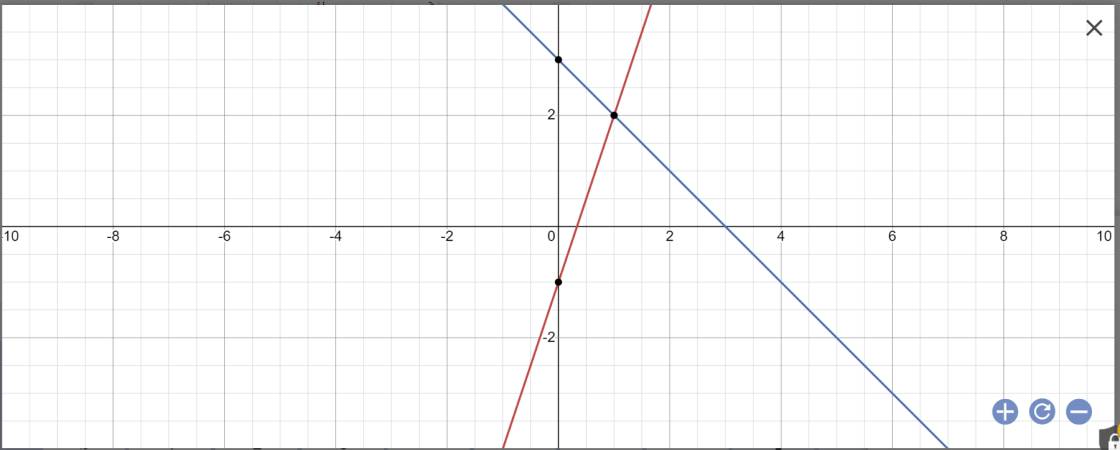
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
Cho x= 0 thì y = 1 ta được điểm (0 ;1)
Cho y = 0 thì x = 1 3 ta được điểm 1 3 ; 0
Vậy tọa độ các giao điểm của đồ thị hàm số y = - 3 x + 1 với các trục Ox, Oy lần lượt là: 1 3 ; 0 và (0;1)