Cho hàm số f x = 1 x ≤ 3 a x + b 3 < x < 5 7 x ≥ 5 . Xác định a; b để hàm số có giới hạn tại x = 3 và x = 5.
A. a = 3; b = -8
B. a = -3; b = 8
C. a = -3; b = -8
D. a = 3; b = 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


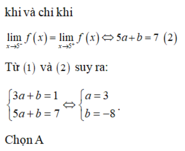

b) ta có: f(2) = 2 - 3 = -1
f(5) = 5 - 3 = 2
f(-1/2) = -1/2 - 3 = -7/2
ko bít đúng ko?? 565464654654654765876546266456456456756756757
a,y = f(x) = x - 3 nếu x =3 hoặc x > 3 và = -(x - 3) nếu x < 3
b,+ Với f(2), ta có: 2 < 3
-> y = f(2) = -(2 - 3) = -(-1) = 1
+ Với f(5), ta có: 5 > 3
-> y = f(5) = 5 - 3 = 2
+ Với f(\(-\frac{1}{2}\)), ta có: \(-\frac{1}{2}\)< 3
-> y = f(\(-\frac{1}{2}\)) = -(\(-\frac{1}{2}\)- 3) = -(\(-3\frac{1}{2}\)) = \(3\frac{1}{2}\)
c, Với f(x) = \(\frac{1}{3}\), ta có:
TH1: x > 3
Ta có:y = f(x) = x - 3 = \(\frac{1}{3}\)
-> x = \(\frac{1}{3}\)+ 3 =



ủng hộ mik nên 100 điểm nha các bạn
mik xin các bạn làm ơn tik mik >_<

1 ) \(f\left(3\right)\Rightarrow x=3\)
Vì \(3< 5\Rightarrow f\left(3\right)=-2.3+7,3=-6+7,3=1,3\)
2 ) Để \(A=x-\left|x\right|\) đạt GTLN <=> \(\left|x\right|\)đạt GTNN
Mà \(\left|x\right|\ge0\forall x\) => \(\left|x\right|\) có GTNN là 0 tại x = 0
=> \(A=x-\left|x\right|\)có GTLN là 0 tại x = 0