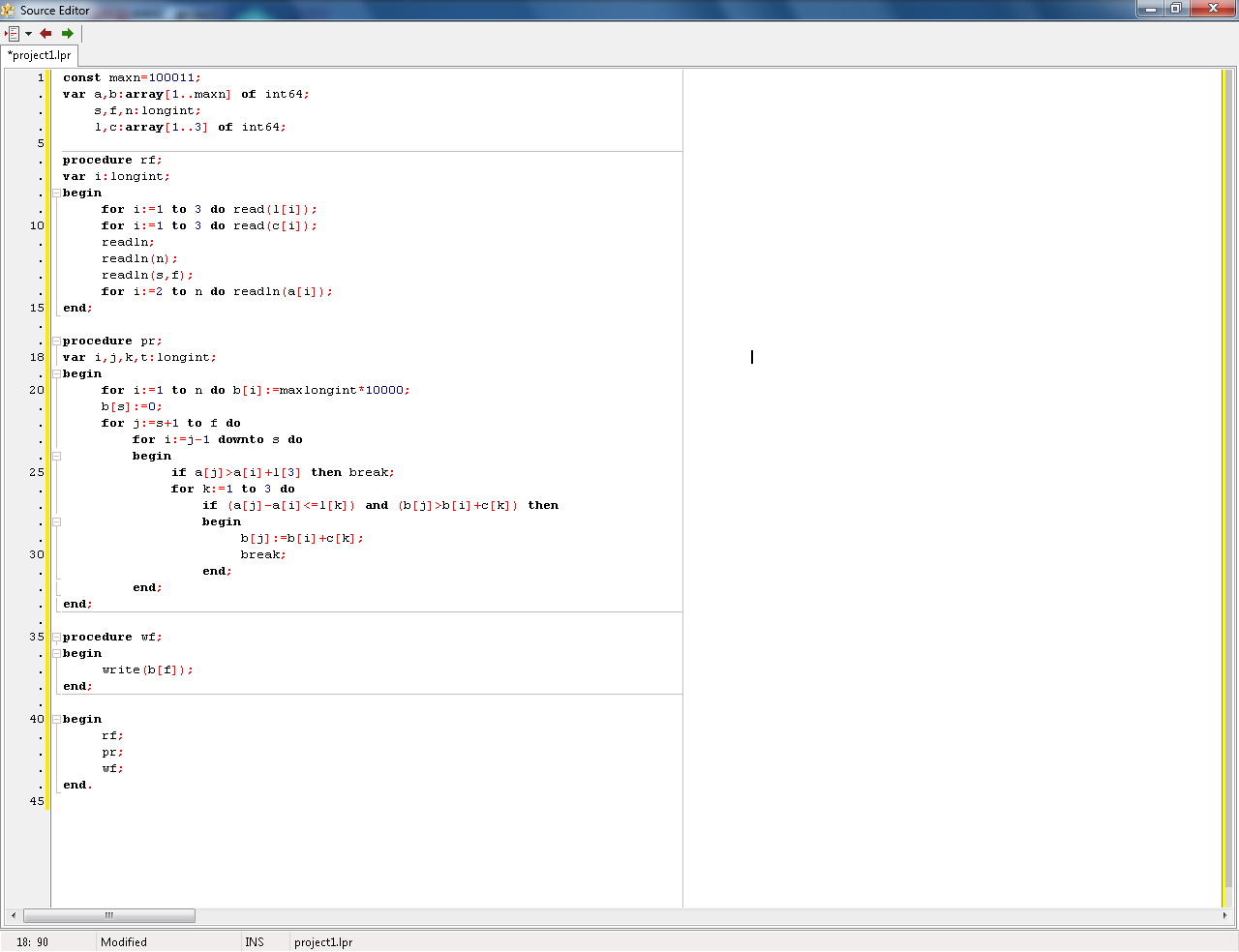
Tuyến đường sắt từ thành phố A đến thành phố B đi qua một số nhà ga. Tuyến đường có thể biểu diễn bởi một đoạn thẳng, các nhà ga là các điểm trên đó. Tuyến đường bắt đầu từ A và kết thúc ở B, vì thế các nhà ga sẽ được đánh số bắt đầu từ A (có số hiệu là 1) và B
là nhà ga cuối cùng.
Giá vé đi lại giữa hai nhà ga chỉ phụ thuộc vào khoảng cách giữa chúng. Cách tính giá vé như sau:
Khoảng cách giữa hai nhà ga (X
)
Khoảng cách 0<X≤
L1 → Giá vé C1
Khoảng cách 0<X≤
L2 → Giá vé C2
Khoảng cách 0<X≤
L3 →
Giá vé C3
Nghĩa là với các giá vé C1
, C2, C3 tương ứng bạn sẽ đi quảng đường tối đa là L1, L2, L3
.
Vé để đi thẳng từ nhà ga này đến nhà ga khác chỉ có thể đặt mua nếu khoảng cách giữa chúng không vượt quá L3
. Vì thế nhiều khi để đi từ nhà ga này đến nhà ga khác ta phải đặt mua một số vé. Hơn thế nữa, nhân viên đường sắt yêu cầu hành khách chỉ được giữ đúng một vé khi đi trên tàu và vé đó sẽ bị huỷ khi hành khách xuống tàu.
Yêu cầu: Tìm cách đặt mua vé để đi lại giữa hai nhà ga cho trước với chi phí mua vé là nhỏ nhất.
Input
Dòng đầu tiên ghi các số nguyên L1
, L2, L3, C1, C2, C3 (1≤ L1 ≤ L2 ≤ L3 ≤109; 1≤ C1 ≤ C2 ≤ C3 ≤109
) theo đúng thứ tự liệt kê ở trên.
Dòng thứ hai chứa số lượng nhà ga N
(2≤N≤100000
)
Dòng thứ ba ghi hai số nguyên s
, f
là các chỉ số của hai nhà ga cần tìm cách đặt mua vé với chi phí nhỏ nhất để đi lại giữa chúng.
Dòng thứ i
trong số N - 1 dòng tiếp theo ghi số nguyên là khoảng cách từ nhà ga A (ga 1) đến nhà ga thứ i + 1
.
Output
Gồm 1
dòng duy nhất ghi chi phí nhỏ nhất tìm được.
Sample Input
3 6 8 20 30 40 7 2 6 3 7 8 13 15 23
Sample Output
70

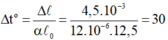
Chọn đáp án C.