Một thỏi hợp kim chì, kẽm có khối lượng 1 kg ở 1250C được thả vào một nhiệt lượng kế có khối lượng 1,6 kg và nhiệt dung riêng 250 J/kg.K chứa 1 kg nước ở 200C. Nhiệt độ khi cân bằng là 250C. Xác định khối lượng chì, kẽm chiếm bao nhiêu phần trăm trong hợp kim. Biết rằng nhiệt dung riêng của chì, kẽm, nước lần lượt là: 130 J/kg.K; 400J/kg.K; 4200J/kg.K (Bỏ qua nhiệt lượng hao phí tỏa vào môi trường xung quanh) giúp mik lời giải chi tiết nhé !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
Phương trình cân bằng nhiệt:
(Cnlk + mncn).(t – t1) = [mkck + (mhk – mk)cch].(t2 – t)
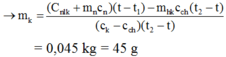
→ mch = mhk – mk = 5 g.

Độ lớn của nhiệt lượng toả ra và nhiệt lượng thu vào :
Q t o ả = c 1 m 1 t 2 - t + c 2 m 2 t 2 - t = c 1 m 1 t 2 - t + c 2 M - m 1 t 2 - t (1)
Q t h u = c m t - t 1 + c 0 m 0 t - t (2)
Từ (1) và (2) dễ dàng tính được :
m 1 = 0,104 kg = 104 g ; m 2 = 0,046 kg = 46 g.

Gọi nhiệt độ cân bằng hệ là \(t^oC\).
\(V=2l\Rightarrow m=2kg\)
Nhiệt lượng quả cầu tỏa ra:
\(Q_{tỏa}=m_1c_1\left(t_1-t\right)=0,5\cdot880\cdot\left(100-t\right)J\)
Nhiệt lượng nước thu vào:
\(Q_{thu}=m_2c_2\left(t-t_2\right)=2\cdot4200\cdot\left(t-20\right)J\)
Cân bằng nhiệt: \(Q_{thu}=Q_{tỏa}\)
\(\Rightarrow2\cdot4200\cdot\left(t-20\right)=0,5\cdot880\cdot\left(100-t\right)\)
\(\Rightarrow t=23,98^oC\)
Nhiệt độ nước sau khi cân bằng:
\(t_{sau}=23,98+20=43,98^oC\)

Nhiệt lượng toả ra :
Q = m 1 c 1 ∆ t + (0,05 - m1 ) c 2 ∆ t (1)
Ở đây m 1 , c 1 là khối lượng và nhiệt dung riêng của kẽm, c 2 là nhiệt dung riêng của chì.
Nhiệt lượng thu vào :
Q' = mc ∆ t' + c' ∆ t' = (mc + c') ∆ t' (2)
Ở đây m, c là khối lượng và nhiệt dung riêng của nước, c' là nhiệt dung riêng của nhiệt lượng kế.
Từ (1) và (2) rút ra :
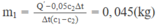
Khối lượng của chì m 2 = 0,05 – m 1 , hay m 2 = 0,005 kg.

Gọi t1 là nhiệt độ ban đầu của miếng hợp kim, ta có t1=1360C
t2 là nhiệt độ ban đầu của nhiệt lượng kế và nước trong nhiệt lượng kế, ta có t2=140C
t=180C - nhiệt độ khi cân bằng trong nhiệt lượng kế
Nhiệt lượng toả ra:
Q Z n = m Z n . C Z n ( t 1 − t ) Q P b = m P b . C P b ( t 1 − t ) ⇔ = m Z n .337. ( 136 − 18 ) = 39766 m Z n = m P b .126. ( 136 − 18 ) = 14868 m P b
Nhiệt lượng thu vào:
Q H 2 O = m H 2 O . C H 2 O ( t − t 2 ) = 100 1000 .4180 ( 18 − 14 ) = 1672 J Q N L K = C ' ( t − t 2 ) = 50. ( 18 − 14 ) = 200 J
Ta có, phương trình cân bằng nhiệt:
Q t o a = Q t h u ↔ 39766 m Z n + 14868 m P b = 1672 + 200 1
Mặt khác, theo đầu bài, ta có:
m Z n + m P b = 50 g = 0 , 05 k g 2
Từ (1) và (2), ta có:
39766 m Z n + 14868 m P b = 1872 m Z n + m P b = 0 , 05 → m Z n = 0 , 045 k g m P b = 4 , 67.10 − 3 ≈ 0 , 005 k g
Đáp án: A

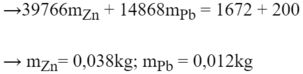
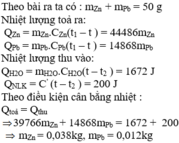

Nhiệt lượng do thỏi hợp kim tỏa ra:
\(Q_1+Q_2=\left(m_1c_1+m_2c_2\right)\left(t_1-t\right)\)
\(=\left(130m_1+400m_2\right)\left(125-25\right)\)
\(=100.\left(130m_1+400m_2\right)J\)
Nhiệt lượng do nhiệt lượng kế và nước thu vào:
\(Q_3+Q_4=\left(m_3c_3+m_4c_4\right)\left(t-t_2\right)\)
\(=\left(1,6\cdot250+1\cdot4200\right)\left(25-20\right)\)
\(=23000J\)
Ta có phương trình cân bằng nhiệt:
\(Q_1+Q_2=Q_3+Q_4\)
\(\Rightarrow100\left(130m_1+400m_2\right)=23000\)
\(\Rightarrow13m_1+40m_2=23\)
Mà \(m_1+m_2=1\)
\(\Rightarrow\left\{{}\begin{matrix}m_1=0,63kg\\m_2=0,37kg\end{matrix}\right.\)
\(\%m_1=\dfrac{0,63}{1}\cdot100\%=63\%\)
\(\%m_2=100\%-63\%=37\text{%}\)