a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.
b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.

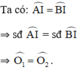
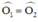 ; OH chung
; OH chung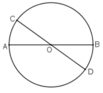
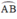 , H = OI ∩ AB.
, H = OI ∩ AB.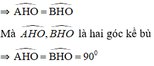
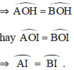
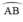
a)
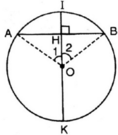
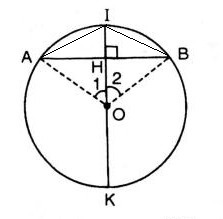
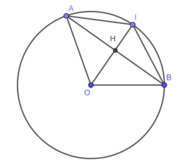
Vẽ đường tròn tâm O, dây cung AB.
Gọi I là điểm chính giữa của cung AB.
Gọi OI ∩ AB = H.
ΔAOH và ΔBOH có: AO = OB, O 1 ^ = O 2 ^ ; OH chung
⇒ ΔAOH = ΔBOH (c-g-c)
⇒ AH = BH (hai cạnh tương ứng)
⇒ OI đi qua trung điểm H của AB.
+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.
Mệnh đề sai
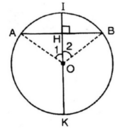
Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.
b)
+ Cho đường tròn (O); dây cung AB ;
I là điểm chính giữa cung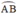 , H = OI ∩ AB.
, H = OI ∩ AB.
⇒ ΔAOH = ΔBOH (cm phần a).
⇒ OH ⊥ AB.
Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.
+ Cho đường tròn (O); dây cung AB.
Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.
Ta có: ΔABO cân tại O (vì AO = OB = R).
⇒ đường cao OH đồng thời là đường phân giác
⇒ I là điểm chính giữa của cung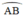
Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.
Kiến thức áp dụng
+ Điểm chính giữa cung là điểm chia cung thành hai cung bằng nhau.