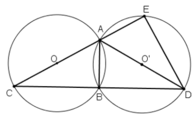
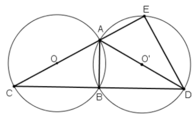
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').
a) So sánh các cung nhỏ BC, BD.
b) Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: BE ^ = BD ^ ) )

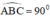
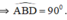
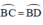 ( định lý )
( định lý )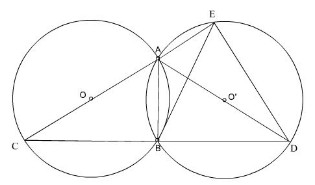
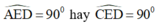
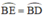 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
a) Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒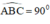
Chứng minh tương tự
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒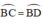 ( định lý )
( định lý )
b) Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒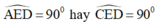
⇒ ΔECD vuông tại E.
Ta có:
Suy ra: C, B, D thẳng hàng.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒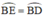 (định lý) hay B là điểm chính giữa cung
(định lý) hay B là điểm chính giữa cung 
Kiến thức áp dụng
+ Với hai cung nhỏ trong cùng một đường tròn hoặc hai đường tròn bằng nhau thì hai dây bằng nhau căng hai cung bằng nhau.