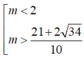
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
Bpt đã cho tương đương với ( 2m+1) x ≥ 5-m (*)
TH1: Với m> -1/2, bpt (*) trở thành: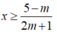 
Tập nghiệm của bpt là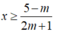 
Để bpt đã cho nghiệm đúng với mọi x:
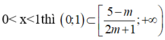
Hay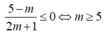 
TH2: nếu m= -1/2 , bpt (*) trở thành: 0x ≥ 5+1/2
Bpt vô nghiệm => không có m thòa mãn
TH3: Với m< -1/2, bpt (*) trở thành: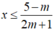 
Tập nghiệm của bpt là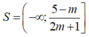 
Để bpt đã cho nghiệm đúng với 0< x< 1 thì
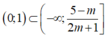
Hay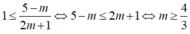 
Kết hợp điều kiện m< -1/2 nên không có m thỏa mãn
Vậy với m≥ 5, bất phương trình đã cho nghiệm đúng với mọi x: 0< x< 1
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
a, Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m-1>0\\\Delta'=m^2-4m+4+m-1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\\left(m-\dfrac{3}{2}\right)^2< -\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
b, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-1\right)x^2+2\left(m-2\right)x-1< 0\) có nghiệm với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m-1< 0\\\Delta'=m^2-3m+3< 0\end{matrix}\right.\)
\(\Leftrightarrow\) vô nghiệm
Vậy không tồn tại giá trị m thỏa mãn
\(\Delta=\left(2m+1\right)^2-4\left(m^2+m-2\right)=9>0;\forall m\)
Phương trình luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m+1\\x_1x_2=m^2+m-2\end{matrix}\right.\)
\(x_1\left(x_1-2x_2\right)+x_2\left(x_2-2x_1\right)=9\)
\(\Leftrightarrow x_1^2+x_2^2-4x_1x_2=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=9\)
\(\Leftrightarrow\left(2m+1\right)^2-6\left(m^2+m-4\right)=9\)
\(\Leftrightarrow2m^2+2m-4=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-2\end{matrix}\right.\)
Chọn A