Cho hình chóp S. ABCD có đáy là một tứ giác lồi. Gọi M và N lần lượt là trọng tâm của tam giác SAB và SAD. Khẳng định nào sau đây là đúng?
A. MN // PQ với P là giao điểm của SM và AB; Q là giao điểm của SN và AD
B. MN, BD chéo nhau.
C. MN và BD cắt nhau.
D. MN là đường trung bình của tam giác IBD với I là trung điểm của SA.

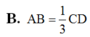
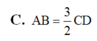
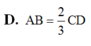
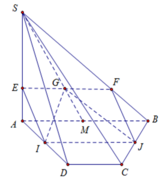


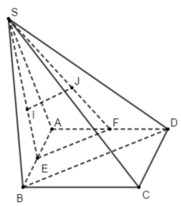

Đáp án A
+) M là trọng tâm của tam giác SAB nên giao điểm P của SM và AB là trung điểm của AB.
Suy ra SM = 2/3 SP ⇒ S M S P = 2 3
N là trọng tâm của tam giác SAD nên giao điểm Q của SN và AD là trung điểm của AD
Suy ra SN = 2/3 SQ ⇒ S N S Q = 2 3
Xét tam giác SPQ có S M S P = S N S Q = 2 3 nên MN // PQ (1) (định lý Ta-lét)
Do đó đáp án A đúng.
+) Xét tam giác IBD có
I M I B = 1 3 (tam giác SAB có I là trung điểm của SA và M là trọng tâm)
I N I D = 1 3 (tam giác SAD có I là trung điểm của SA và N là trọng tâm)
Do đó I M I B = I N I D = 1 3 nên MN // BD
Suy ra đáp án B, C, D sai.
Chọn đáp án A