Chứng minh rằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

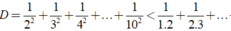
![]()
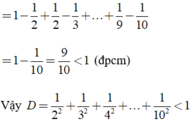

a>
\(\frac{1}{2^2}+\frac{1}{100^2}\)=1/4+1/10000
ta có 1/4<1/2(vì 2 đề bài muốn chứng minh tổng đó nhỏ 1 thì chúng ta phải xét xem có bao nhiêu lũy thừa hoặc sht thì ta sẽ lấy 1 : cho số số hạng )
1/100^2<1/2
=>A<1


Ta có : D = \(\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{10^2}=\frac{1}{2.2}+\frac{1}{3.3}+...+\frac{1}{10.10}< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{9.10}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{9}-\frac{1}{10}=1-\frac{1}{10}< 1\)
=> D < 1 (đpcm)
Ta có : \(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^3}< \frac{1}{2.3}\)
\(\frac{1}{4^2}< \frac{1}{3.4}\)
...
\(\frac{1}{10^2}< \frac{1}{9.10}\)
=)) \(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{10^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{9.10}\)
Mà \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}\)
\(=1-\frac{1}{10}=\frac{9}{10}< 1\)
=)) A < 1 (đpcm)

A la dat tren tong
We have: A = 1/2 ^ 2 + 1/3 ^ 2 + 1/4 ^ 2 + ........... + 1/10 ^ 2
A = 1 / 2.2 + 1 / 3.3 + 1 / 4.4 + ....... + 1 / 10:10
A <1 / 1.2 + /2.3 + 1/3.4 +......+1/9.10
A < 1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ....+ 1/9 - 1/10
A < 1-1/10
Ma 1 - 1/10 = 9/10 < 1
=>A < 1 (dpcm)
dễ
1/2^2=1/1.2
1/3^2=1/2.3
1/4^2=1/3.4
....
1/10^2=1/9.10
1/1.2+1/2.3+1/3.4+...+1/9.10
=(1-1/2+1/2-1/3+1/3-1/4+...+1/9-1/10)
=1-1/10
=9/10




ta có:
\(\frac{1}{3^2}=\frac{1}{3\cdot3}< \frac{1}{2\cdot3}\),
\(\frac{1}{4^2}=\frac{1}{4\cdot4}< \frac{1}{3\cdot4}...\)
\(\frac{1}{10^2}=\frac{1}{10\cdot10}< \frac{1}{9\cdot10}\)
Từ trên => A < \(\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+...+\frac{1}{9\cdot10}\)
=> \(A< \frac{1}{2}-\frac{1}{3}+\frac{1}{3}-...+\frac{1}{9}-\frac{1}{10}\)
=> \(A< \frac{1}{2}-\frac{1}{10}=\frac{5}{10}-\frac{1}{10}=\frac{4}{10}=\frac{2}{5}\)
=> \(A< \frac{2}{5}\)mà \(\frac{2}{5}< \frac{1}{2}\)
=> \(A< \frac{1}{2}\)=> \(\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{10^2}< \frac{1}{2}\)
Chúc bn học tốt !