Cho Δ A B C = Δ H I K biết A ^ + H ^ = 80 ° , I ^ = 70 ° . Số đo góc C ^ là:
A. C ^ = 30 °
B. C ^ = 40 °
C. C ^ = 50 °
D. C ^ = 70 °
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
1 tháng 6 2019
Đúng(0)
Những câu hỏi liên quan
29 tháng 8 2021
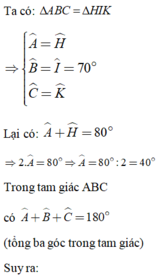
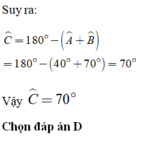
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền BA, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
18 tháng 2 2017
TA CÓ TAM GIÁC ABC VUÔNG TẠI B , AD ĐL PYTAGO TA CÓ
\(AB^2+BC^2=AC^2\)
=>\(8^2+15^2=289=>AC^{ }=17\)
=>AC=17 CM
1 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
b: BH=BC/2=3(cm)
=>AH=4(cm)
c: Ta có: AH là đường trung tuyến
mà AG là đường trung tuyến
nên A,H,G thẳng hàng
d: Xét ΔABG và ΔACG có
AB=AC
\(\widehat{BAG}=\widehat{CAG}\)
AG chung
Do đó: ΔABG=ΔACG
KP
20 tháng 4 2022
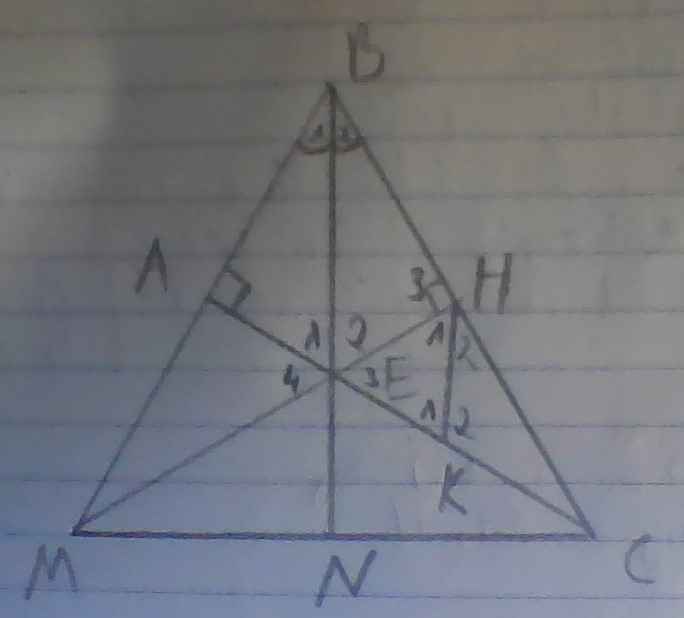
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC
16 tháng 4 2021
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}+60^0=90^0\)
hay \(\widehat{C}=30^0\)
Vậy: \(\widehat{C}=30^0\)
16 tháng 4 2021
a) Xét ΔABC có \(\widehat{C}< \widehat{B}< \widehat{A}\left(30^0< 60^0< 90^0\right)\)
mà cạnh đối diện với góc C là cạnh AB
và cạnh đối diện với góc B là cạnh AC
và cạnh đối diện với góc A là cạnh BC
nên AB<AC<BC(đpcm)