Cho mạch như hình vẽ:
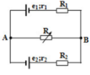
E 1 = 12 V , E 2 = 6 V , r 1 = r 2 = 0 , 5 Ω ; R 1 = 4 , 5 Ω ; R 2 = 2 , 5 Ω . R là biến trở. Với giá trị nào của biến trở thì công suất trên R đạt cực đại, giá trị cực đại đó là?
A. 3 4 W
B. 1 40 W
C. 3 40 W
D. 4 3 W
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điểm D và G có cùng hiệu điện thế nên chập D và G lại mạch như hình vẽ.
Tổng trở mạch ngoài: R n g = R 1 + R 2 . R 3 R 2 + R 3 = 24 Ω
Dòng điện trong mạch chính: I = E R n g + r = 30 25 = 1 , 2 ( A )
Ta có: I1 = I23 = I = 1,2 (A)
Hiệu điện thế giữa hai điểm D và B: U D B = U 23 = I . R 23 = 14 , 4 ( V )
Hiệu điện thế giữa hai đầu R2: U 2 = U 23 = 14 , 4 ( V )
Dòng điện qua R2: I 2 = U 2 R 2 = 14 , 4 36 = 0 , 4 ( A )
Dựa vào mạch gốc ta thấy: I 1 = I 2 + I A ⇒ I A = I 1 − I 2 = 1 , 2 − 0 , 4 = 0 , 8 ( A )
Chọn B

\(\xi=\xi_1+\xi_2=12+12=24V\)
\(r=n\cdot r=2\cdot0,5=1\Omega\)
\(R_Đ=\dfrac{U_Đ^2}{P_Đ}=\dfrac{6^2}{9}=4\Omega\)
\(R_{3Đ}=R_3+R_Đ=6+4=10\Omega\)
\(R_N=\dfrac{R_1\cdot R_{3Đ}}{R_1+R_{3Đ}}=\dfrac{10\cdot10}{10+10}=5\Omega\)
\(I=\dfrac{\xi}{r+R_N}=\dfrac{24}{1+5}=4A\)

Dòng điện qua mạch:
\(I=\dfrac{\xi}{r+R}=\dfrac{12}{2+R}\)
Công suất nguồn:
\(P=\xi\cdot I=12\cdot\dfrac{12}{2+R}=24W\)
\(\Rightarrow R=4\Omega\)
Chọn D.

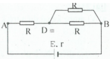
Công thức ta có:
\(I=\dfrac{\xi}{r+R}=\dfrac{14}{3+4}=2A\)
\(U_{AB}=R\cdot I\) hoặc có tính theo công thức \(U_{AB}=\xi-I\cdot r\)
\(\Rightarrow U_{AB}=\xi-I\cdot r=14-2\cdot3=8V\)
Chọn C.
Đáp án cần chọn là: C