Trong hình bình hành: hình lục giác đều có bao nhiêu trục đối xứng và bao nhiêu tâm đối xứng?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2021
Hình bình hành = 0 trục
hình chữ nhật = 2 trục
hình vuông = 4 trục
hình lục giác đều = 6 trục
hình thoi = 2 trục
xin like
29 tháng 11 2018
Tứ giác: 0 trục, 0 tâm
Hình thang 0 trục, 0 tâm
Hình thang cân 1 trục 0 tâm
Hình bình hành 0 trục 1 tâm
Hình chữ nhật 2 trục 1 tâm
Hình thoi 2 trục 1 tâm
Hình vuông 4 trục 1 tâm
5 tháng 10 2022
Tứ giác: 0 trục đối xứng, 0 tâm đối xứng
Hình thang: 0 trục đối xứng, 0 tâm đối xứng
Hình thang cân: 1 trục đối xứng, 0 tâm đối xứng
Hình bình hành: 0 trục đối xứng, 1 tâm đối xứng
Hình chữ nhật: 2 trục đối xứng, 1 tâm đối xứng
Hình thoi: 2 trục đối xứng, 1 tâm đối xứng
Hình vuông: 4 trục đối xứng, 1 tâm đối xứng
Tích đúng 5 sao cho mình nhé.
OK bạn
2 tháng 12 2023
Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
QT
1
NK
3
30 tháng 12 2022
hình vuông có 4 trục đối xứng
hình tròn có vô số trục đối xứng
hình tam giác đều có 3 trục đối xứng
hình lục giác đều có 6 trục đối xứng
30 tháng 12 2022
hình vuông có : 4 trục đối xứng
hình tam giác đều có: 3 trục đối xứng
hình tròn rất nhiều trục đối xứng
hình lục giác đều có : 6 trục đối xứng
HT
PT
1
CM
29 tháng 7 2017
Tam giác đều và ngũ giác dều không có tâm đối xứng.
* Hình bình hành có một tâm đối xứng là giao điểm của hai đường chéo.
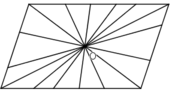
* Hình lục giác đều có một tâm đối xứng, đó là tâm đường tròn ngoại tiếp hình lục giác đều.
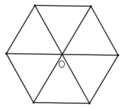
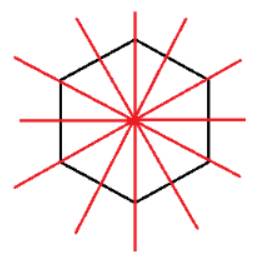
Một cách tổng quát : Có hai loại tứ giác có trục đối xứng.
1. Tứ giác có hai đường trung trực của hai cạnh đối diện nhau trùng nhau.
2. Tứ giác có 4 đỉnh nằm trên hai đường thẳng vuông góc với nhau và không có hai đỉnh kề nhau nằm trên cùng một trong hai đường thẳng đó.
Chưa xét tứ giác lõm.