Cho hàm số y=f(x) liên tục trên ℝ và có bảng xét dấu của đạo hàm như hình bên. Hàm số đã cho có bao nhiêu điểm cực trị?
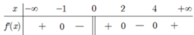
A. 3
B. 2
C. 1
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Dựa vào bảng xét dấu f ' (x) ta có: hàm số f(x) liên tục trên ℝ có 4 điểm x o mà tại đó f ' (x) đổi dấu khi x qua điểm x o . Vậy hàm số đã cho có 4 điểm cực trị

Chọn A.
Phương pháp:
Điểm x = x0 là điểm cực trị của hàm số khi qua điểm đó f'(x) đổi dấu.
Cách giải :
Dựa vào BXD ta thấy hàm số có 4 điểm cực trị x = -1; x = 0; x = 2; x = 4.
Chú ý: Nhiều học sinh cho rằng x = 0 không phải là điểm cực trị do y' (0) ≠ 0. Lưu ý điều kiện f'(x0) = 0
chỉ là điều kiện cần để x = x0 là điểm cực trị của hàm số.

Nhận thấy y' đổi dấu khi qua x = -3 và x = 2 nên hàm số có 2 điểm cực trị. ( x = 1 không phải là điểm cực trị vì y' không đổi dấu khi qua x = 1). Chọn C.
Đáp án D
Dựa vào bảng xét dấu ta thấy hàm số đổi dấu qua các điểm x = − 1 , x = 0 , x = 2 , x = 4 nên hàm số có 4 điểm cực trị.