Trong không gian hệ trục tọa độ Oxyz, cho mặt phẳng P : 1 − m 2 2 n x + 4 m n y + 1 + m 2 1 − n 2 z + 4 m 2 + n 2 + m 2 n 2 + 1 = 0 . Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là
A. 1
B. 2
C. 3
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
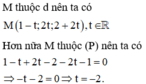
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Chọn B

Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).
Đáp án D
Hướng giải: Ta sẽ đi tìm 1 mặt phẳng song song với (P), đồng thời tiếp xúc với mặt cầu. Lúc này, khoảng cách giữa 2 mặt phẳng này chính là 2 lần bán kính mặt cầu.
Do (P) luôn tiếp xúc với 1 mặt cầu cố định => Ta chọn tùy ý m, n để được 2 mặt phẳng song song
+ Chọn m=1,n=1 =>4y+16=0 => y = - 4 ( α 1 )
+ Chọn m=-1,n=1 => -4y+16=0 => y=4 ( α 2 )
d ( ( α 1 ) , ( α 2 ) ) = 8 = > r = 4