Cho số phức z thoả mãn z - 1 ≤ 1 và z - z ¯ có phần ảo không âm. Tập hợp các điểm biểu diễn số phức z là một miền phẳng. Tính diện tích S của miền phẳng này
A. S = π
B. S = 2 π
C. S = 1 2 π
D.S = 1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đường phân giác của góc phần tư thứ nhất và góc pần tư thứ ba.
b) Đường phân giác của góc phần tư thứ hai và góc phần tư thứ tư.
c) Đường thẳng y = 2x + 1
d) Nửa đường tròn tâm O bán kính bằng 1, nằm bên phải trục Oy.

Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A(-1;3) thì theo điều kiện, ta có: ![]()
Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
![]()

Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A − 1 ; 3 thì theo điều kiện, ta có: 3 ≤ z − 3 i + 1 ≤ 5 ⇔ 3 ≤ A M ≤ 5. Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
⇒ S = π 5 2 − 3 3 = 16 π .

Đáp án D.
Gọi M là điểm biểu diễn của số phức z. Xét điểm A(-1;3) thì theo điều kiện, ta có
![]()
Vậy tập hợp các điểm biểu diễn z là phần hình phẳng nằm giữa 2 đường tròn tâm A, bán kính lần lượt là 3 và 5
![]()

Chọn A.
+ Giả sử z = a + bi, khi đó ![]() , giả thiết của bài toán là
, giả thiết của bài toán là
![]()
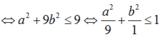
+ Vậy tập hợp các điểm biểu diễn cho số phức z là điểm M(a; b) thuộc miền trong của elip 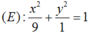 (kể cả các điểm trên biên).
(kể cả các điểm trên biên).
+ Bán trục lớn của ( E) là a = 3, bán trục bé của ( E) là b = 1 nên diện tích cần tính của miền ( H) là S = πab = 3π.