Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng 2. Gọi M,N,P lần lượt là trung điểm các cạnh AB,BB′ và A’C’ (tham khảo hình vẽ bên). Thể tích của khối tứ diện CMNP bằng
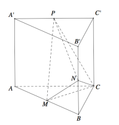
A. 5 3 12
B. 2 3 3
C. 5 3 4
D. 5 3 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
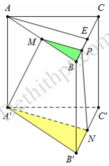
Gọi E là trung điểm của BC, F là trung điểm của BE
Khi đó M F / / A E mà A E / / A ' N nên M F / / A ' N
Suy ra các điểm A ' , M , F , N thuộc cùng một mặt phẳng
Vậy A ' M N cắt cạnh BC tại P ⇒ P trùng với F
Công thức tổng quát tính thể tích khối đa diện
“thể tích khối chóp cụt là V = h 3 B + B ' + B B ' với h là chiều cao, B, B’ lần lượt là diện tích hai đáy”
Và diện tích đáy B = S M B P = S A B C 8 = S 8 B ' = S A ' B ' N = S A ' B ' C ' 2 = S 2 với S = a 2 3 4
⇒ Thể tích khối đa diện M N P . A ' B ' N là V = B B ' 3 S 8 + S 2 + S 8 . S 2 = 7 3 a 3 96

Đáp án B
Tọa độ hóa với O ≡ N , O x ≡ N B ' , O y ≡ N A ' , O z ≡ N K và chuẩn hóa vớí a = 2 .
Ta có
A ' 0 ; 3 ; 0 , A 0 ; 3 ; 2 B 1 ; 0 ; 2 ⇒ M 1 2 ; 3 2 ; 2
⇒ N A ' → = 0 ; 3 ; 0 N M → = 1 2 ; 3 2 ; 2 ⇒ n A ' M N → = N A ' → . N M → = 2 3 ; 0 ; − 3 2
⇒ A ' M N : 4 x − z = 0
Lại có
B 1 ; 0 ; 2 , K 0 ; 0 ; 2 ⇒ K B → = 1 ; 0 ; 0 ⇒ B C : x = t y = 0 z = 2
Mà
P = B C ∩ A ; M N ⇒ P 1 2 ; 0 ; 2
V M B P . A ' B ' N ' = V M . A ' B ' N + V M . B P N B = V A . A ' B ' N + 1 2 V A . B P N B ' V A . A ' B ' N = 1 2 V A . A ' B ' C ' = 1 6 V A B C . A ' B ' C ' S B P N B ' = 1 2 S B C C ' B ' − S N P K = 1 2 S B C C ' B ' − 1 8 S B C C ' B ' = 3 8 S B C C ' B ' = 3 4 S B C B ' ⇒ V A . B P N B ' = 3 4 V A . B C B ' = 1 4 V A B C . A ' B ' C ' ⇒ V M B P . A ' B ' N = 7 24 V A B C . A ' B ' C ' = 7 24 A ' A . S A B C = 7 24 a . a 2 3 4 = 7 a 3 3 96
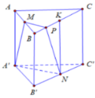

Đáp án A
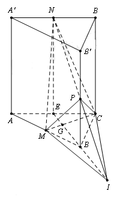
Gọi E là trung điểm của A C ⇒ N E / / B B ' . Nối NP cắt BE tại I suy ra B là trung điểm của EI. Gọi G là trọng tâm của tam giác ABC ⇒ B G = 2 E G .
⇒ d B ; M C = 2 d E ; M C ⇒ d B ; M C = 2 3 d B ; A C
Suy ra: d I ; M C = 1 + 3 2 d B ; M C = 5 2 d B ; M C
Mà S Δ I M C = 1 2 d I ; M C . M C
= 1 2 . 5 2 d B ; M C . M C = 5 2 S Δ M B C = 5 4 S Δ A B C
Ta có: V N . M P C V N . M I C = N P N I = 1 2 ⇒ V N . M P C = 1 2 x V N . M I C 1
Lại có:
V N . M I C = 1 3 . d N ; A B C . S Δ I M C = 1 3 . d A ' ; A B C . 5 4 S Δ A B C ⇒ V N . M I C = 5 12 . d A ' ; A B C . S Δ A B C = 5 12 V A B C . A ' B ' C ' = 5 12 V
Từ (1) và (2) suy ra V C M N P = 1 2 . 5 12 x V = 5 24 V .