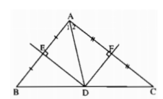
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:
D là trung điểm của cạnh BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Xét tam giác ADE và BDE có:
DE chung
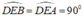
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
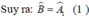
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
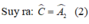
Từ (1) và (2) suy ra: 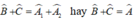

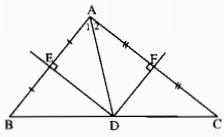
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC

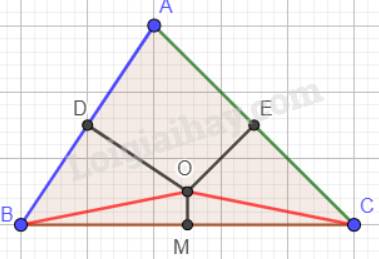
a) Ta có: đường trung trực của hai cạnh AB và AC cắt nhau tại O và O nằm trong tam giác. Nên O là giao điểm của ba đường trung trực của tam giác ABC.
Mà M là trung điểm của cạnh BC nên OM là đường trung trực của đoạn thẳng BC hay \(OM \bot BC\).
b) Ta có: Giao của ba đường trung trực trong tam giác thì cách đều ba đỉnh của tam giác đó.
Hay OB = OC nên tam giác OBC cân tại O. Suy ra: \(\widehat {OBC} = \widehat {OCB}\) hay \(\widehat {OBM} = \widehat {OCM}\). ( tính chất tam giác cân)
Xét tam giác OMB và tam giác OMC có:
OB = OC;
\(\widehat {OBM} = \widehat {OCM}\);
MB = MC (M là trung điểm của đoạn thẳng BC).
Vậy \(\Delta OMB = \Delta OMC\)(c.g.c)
Do đó,\(\widehat {MOB} = \widehat {MOC}\) ( 2 góc tương ứng).


a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.

Xét hai tam giác ABE và DCE có AB=DC (giả thiết), BE=CE (vì E nằm trên trung trực BC) và EA=ED (vì E nằm trên trung trực CD). Suy ra hai tam giác bằng nhau theo trường hợp c.c.c. Từ đó suy ra góc ABE= góc DCE = góc ACE. Vậy B,C nhìn AE dưới hai góc bằng nhau, do đó ABCE nội tiếp. Suy ra E nằm trên đường tròn ngoại tiếp tam giác ABC.

Lời giải:
Vì $M$ nằm trên trung trực của $BC$ nên $MB=MC$. $M$ nằm trên đường trung trực của $AB$ nên $MA=MB$
$\Rightarrow MA=MB=MC$
Xét tam giác $AMC$ và $AMB$ có:
$AM$ chung
$AC=AB$ (do $ABC$ là tam giác cân tại $A$)
$MB=MC$
$\Rightarrow \triangle AMC=\triangle AMB$ (c.c.c)
$\Rightarrow \widehat{ACM}=\widehat{ABM}$
Hay $\widehat{ECM}=\widehat{ABM}$
Mà $\widehat{ABM}=\widehat{MAB}$ (do tam giác $MAB$ cân tại $M$ vì $MA=MB$)
$\Rightarrow \widehat{ECM}=\widehat{MAB}=\widehat{DAM}$
Xét tam giác $ECM$ và $DAM$ có:
$EC=DA$ (gt)
$\widehat{ECM}=\widehat{DAM}$ (cmt)
$CM=AM$ (cmt)
$\Rightarrow \triangle ECM=\triangle DAM$ (c.g.c)
$\Rightarrow ME=MD$ (đpcm)
Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.