Cho hàm số y = - 1 2 x + 3
Hàm số đã cho là hàm số đồng biến hay nghịch biến? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
11 tháng 9 2019
Hàm số y = (3 - 2 )x + 1 có hệ số a = 3 - 2 , hệ số b = 1
Ta có: a = 3 - 2 > 0 nên hàm số đồng biến trên R
NK
1
3 tháng 1 2022
\(\text{Ta có:}-m^2+m-4\\ =-\left(m^2-m+4\right)\\ =-\left[\left(m^2-m+\dfrac{1}{4}\right)+\dfrac{15}{4}\right]\\ =-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}\le-\dfrac{15}{4}< 0\)
Vậy HSNB trên R
3 tháng 1 2022
\(-m^2+m-4\)
\(=-\left(m^2-m+4\right)\)
\(=-\left(m^2-m+\dfrac{1}{4}+\dfrac{15}{4}\right)\)
\(=-\left(m-\dfrac{1}{2}\right)^2-\dfrac{15}{4}< 0\forall m\)
Vậy: Hàm số nghịch biến trên R
24 tháng 10 2021
Vì \(-4< 0\) nên \(y=f\left(x\right)=-4x+3\) nghịch biến trên R
Vì \(\dfrac{1}{4}>0\) nên \(y=g\left(x\right)=\dfrac{1}{4}x-6\) đồng biến trên R
CM
25 tháng 4 2018
Ta có:
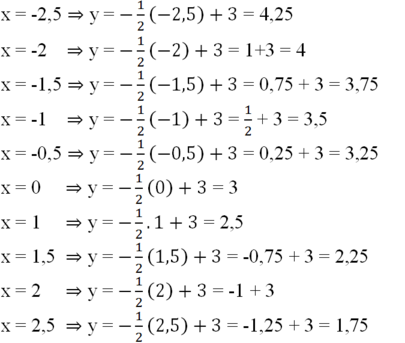
Ta được bảng sau:
b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.
25 tháng 12 2023
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
PN
2
10 tháng 2 2021
Hàm số \(y=\left(\sqrt{3}-2\right)x-1\) là nghịch biến vì \(\sqrt{3}-2=\sqrt{3}-\sqrt{4}< 0\)
Hàm số \(y=\left(\sqrt{3}-1\right)x-5\) là đồng biến vì \(\sqrt{3}-1>0\)
10 tháng 2 2021
a) Hàm số \(y=\left(\sqrt{3}-2\right)x-1\) nghịch biến trên R vì \(\sqrt{3}-2< 0\)
b) Hàm số \(y=\left(\sqrt{3}-1\right)x-5\) đồng biến trên R vì \(\sqrt{3}-1>0\)
Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.