Cho biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

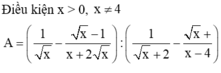
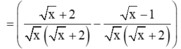
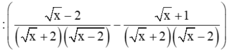
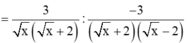
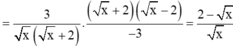
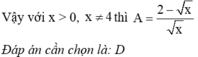

Bài 1:
a: \(Q=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\left(x+\sqrt{x}\right)\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\sqrt{x}\left(\sqrt{x}+1\right)\)
\(=\dfrac{2x}{x-1}\)

1,
\(A=\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{4x^2+x-2-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4x^2-4}{\left(x-2\right)\left(x+2\right)}\)
\(x=4\Rightarrow A=\dfrac{4.x^2-4}{\left(4-2\right)\left(4+2\right)}=...\)
2.
\(A=\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{3\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{3-5x}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x\left(x+1\right)+3\left(x-1\right)+3-5x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x-1}{x+1}\)
3.
Đề lỗi, thiếu dấu trước \(\dfrac{6+5x}{4-x^2}\)
4.
\(A=\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{2x-5\left(x+5\right)-\left(x-5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4x-20}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4}{x-5}\)
\(x=\dfrac{4}{5}\Rightarrow A=\dfrac{-4}{\dfrac{4}{5}-5}=\dfrac{20}{21}\)
5.
\(M=\dfrac{x^2}{x\left(x+2\right)}+\dfrac{2x}{x\left(x+2\right)}+\dfrac{2\left(x+2\right)}{x\left(x+2\right)}\)
\(=\dfrac{x^2+2x+2\left(x+2\right)}{x\left(x+2\right)}=\dfrac{x^2+4x+4}{x\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)^2}{x\left(x+2\right)}=\dfrac{x+2}{x}\)
\(x=-\dfrac{3}{2}\Rightarrow M=\dfrac{-\dfrac{3}{2}+2}{-\dfrac{3}{2}}=-\dfrac{1}{3}\)

Bài 1:
a: \(A=\dfrac{x^2-3+x+3}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}=\dfrac{x\left(x+1\right)}{x\left(x-3\right)}=\dfrac{x+1}{x-3}\)
b: Để A=3 thì 3x-9=x+1
=>2x=10
hay x=5
Bài 2:
a: \(A=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x+2-x}{x+2}\)
\(=\dfrac{-6}{x-2}\cdot\dfrac{1}{2}=\dfrac{-3}{x-2}\)
b: Để A nguyên thì \(x-2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{3;1;5;-1\right\}\)

a: \(A=\left(\dfrac{2x^2+2}{x^3-1}+\dfrac{x^2-x+1}{x^4+x^2+1}-\dfrac{x^2+3}{x^3-x^2+3x-3}\right):\dfrac{1}{x-1}\)
\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{x^4+2x^2+1-x^2}-\dfrac{x^2+3}{x^2\left(x-1\right)+3\left(x-1\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+2}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{\left(x^2-x+1\right)}{\left(x^2+1\right)^2-x^2}-\dfrac{x^2+3}{\left(x-1\right)\left(x^2+3\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{x^2-x+1}{\left(x^2+1+x\right)\left(x^2+1-x\right)}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)
\(=\left(\dfrac{2x^2+3}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{1}{x^2+x+1}-\dfrac{1}{x-1}\right)\cdot\dfrac{x-1}{1}\)
\(=\dfrac{2x^2+3+x-1-x^2-x-1}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x-1}{1}\)
\(=\dfrac{x^2+1}{x^2+x+1}\)
b: Để A là số nguyên thì \(x^2+1⋮x^2+x+1\)
=>\(x^2+x+1-x⋮x^2+x+1\)
=>\(x⋮x^2+x+1\)
=>\(x^2+x⋮x^2+x+1\)
=>\(x^2+x+1-1⋮x^2+x+1\)
=>\(-1⋮x^2+x+1\)
=>\(x^2+x+1\in\left\{1;-1\right\}\)
=>\(x^2+x+1=1\)
=>x2+x=0
=>x(x+1)=0
=>\(x\in\left\{0;-1\right\}\)

a, ĐKXĐ:\(\left\{{}\begin{matrix}x^2-1\ne0\\x+1\ne0\\x-1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne\pm1\\x\ne-1\\x\ne1\end{matrix}\right.\Leftrightarrow x\ne\pm1\)
b, \(P=\dfrac{2x^2}{x^2-1}+\dfrac{x}{x+1}-\dfrac{x}{x-1}\)
\(\Rightarrow P=\dfrac{2x^2}{\left(x+1\right)\left(x-1\right)}+\dfrac{x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\dfrac{x\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2}{\left(x+1\right)\left(x-1\right)}+\dfrac{x^2-x}{\left(x+1\right)\left(x-1\right)}-\dfrac{x^2+x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2+x^2-x-x^2-x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x^2-2x}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)
\(\Rightarrow P=\dfrac{2x}{x+1}\)
c, Thay x=2 vào P ta có:
\(P=\dfrac{2x}{x+1}=\dfrac{2.2}{2+1}=\dfrac{4}{3}\)
Bài `1:`
`a)`
Để `P` có nghĩa thì:
`{(x^2-1\ne0),(x+1\ne0),(x-1\ne0):}`
`<=>x\ne+-1`
`b)`
`P=(2x^2)/(x^2-1)+x/(x+1)-x/(x-1)(x\ne+-1)`
`P=(2x^2)/((x-1)(x+1))+(x.(x-1))/((x+1)(x-1))-(x.(x+1))/((x-1)(x+1))`
`P=(2x^2+x^2-x-x^2-x)/((x-1)(x+1))`
`P=(2x^2-2x)/((x-1)(x+1))`
`P=(2x.(x-1))/((x-1)(x+1))=2x/(x+1)`
`c)`
Với `x=2`
`P=(2.2)/(2+1)=4/3`

a, ĐKXĐ : \(\left\{{}\begin{matrix}x\ne0\\x\ne\pm1\end{matrix}\right.\)
Ta có : \(A=\left(\dfrac{x}{x-1}-\dfrac{1}{x^2-x}\right):\left(\dfrac{1}{x+1}+\dfrac{2}{x^2-1}\right)\)
\(=\left(\dfrac{x}{x-1}-\dfrac{1}{x\left(x-1\right)}\right):\left(\dfrac{1}{x+1}+\dfrac{2}{\left(x-1\right)\left(x+1\right)}\right)\)
\(=\left(\dfrac{x^2-1}{x\left(x-1\right)}\right):\left(\dfrac{x-1+2}{\left(x-1\right)\left(x+1\right)}\right)\)\(=\dfrac{\left(x-1\right)\left(x+1\right)}{x\left(x-1\right)}:\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x+1}{x}:\dfrac{1}{x-1}=\dfrac{x+1}{x}.\left(x-1\right)=\dfrac{x^2-1}{x}\)
b, Thay x = 0,5 vào A ta được : A = -3/2
Vậy ...
a) Ta có: \(A=\left(\dfrac{x}{x-1}-\dfrac{1}{x^2-x}\right):\left(\dfrac{1}{x+1}+\dfrac{2}{x^2-1}\right)\)
\(=\left(\dfrac{x^2}{x\left(x-1\right)}-\dfrac{1}{x\left(x-1\right)}\right):\left(\dfrac{x-1}{\left(x+1\right)\left(x-1\right)}+\dfrac{2}{\left(x+1\right)\left(x-1\right)}\right)\)
\(=\dfrac{x^2-1}{x\left(x-1\right)}:\dfrac{x-1+2}{\left(x+1\right)\left(x-1\right)}\)
\(=\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}\cdot\dfrac{\left(x+1\right)\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2-1}{x}\)
b) Thay \(x=\dfrac{1}{2}\) vào A, ta được:
\(A=\left(\dfrac{1}{4}-1\right):\dfrac{1}{2}=\dfrac{-3}{4}\cdot2=-\dfrac{3}{2}\)
Vậy: Khi \(x=\dfrac{1}{2}\) thì \(A=-\dfrac{3}{2}\)

a) \(A=\dfrac{x-2}{x}=\dfrac{\dfrac{2}{3}-2}{\dfrac{2}{3}}\)\(=-2\)
b)\(B=\dfrac{4x}{x+1}+\dfrac{x}{1-x}+\dfrac{2x}{x^2-1}\left(ĐK:x\ne\pm1\right)\)
\(=\dfrac{4x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}-\dfrac{x\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x\left(x-1\right)-x\left(x+1\right)+2x}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{4x^2-4x-x^2-x+2x}{\left(x-1\right)\left(x+1\right)}\)\(=\dfrac{3x^2-3x}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{3x}{x+1}\)

\(ĐKXĐ:\hept{\begin{cases}x\ne\pm1\\x\ne-\frac{1}{2}\end{cases}}\)
a) \(A=\left(\frac{1}{x-1}+\frac{x}{x^3-1}\cdot\frac{x^2+x+1}{x+1}\right):\frac{2x+1}{x^2+2x+1}\)
\(\Leftrightarrow A=\left(\frac{1}{x-1}+\frac{x}{\left(x-1\right)\left(x+1\right)}\right):\frac{2x+1}{\left(x+1\right)^2}\)
\(\Leftrightarrow A=\frac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\frac{\left(x+1\right)^2}{2x+1}\)
\(\Leftrightarrow A=\frac{\left(2x+1\right)\left(x+1\right)}{\left(x-1\right)\left(2x+1\right)}\)
\(\Leftrightarrow A=\frac{x+1}{x-1}\)
b) Thay \(x=\frac{1}{2}\)vào A, ta được :
\(A=\frac{\frac{1}{2}+1}{\frac{1}{2}-1}=\frac{\frac{3}{2}}{-\frac{1}{2}}=-3\)

\(A=\dfrac{x+2+x-2+x^2+1}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x+1\right)^2}{\left(x-2\right)\left(x+2\right)}\)
Với \(-2< x< 2\Leftrightarrow\left\{{}\begin{matrix}x-2< 0\\x+2>0\end{matrix}\right.\Leftrightarrow\left(x-2\right)\left(x+2\right)< 0;x\ne-1\Leftrightarrow\left(x+1\right)^2>0\Leftrightarrow A< 0\)
\(A=\dfrac{x+2+x-2+x^2+1}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+2x+1}{x^2-4}\)
