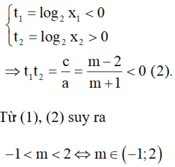Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
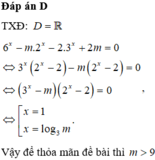
Bài 1 : a, Thay m = -2 vào phương trình ta được :
\(x^2+8x+4+6+5=0\Leftrightarrow x^2+8x+15=0\)
Ta có : \(\Delta=64-60=4>0\)
Vậy phương trình có 2 nghiệm phân biệt
\(x_1=\frac{-8-2}{2}=-5;x_2=\frac{-8+2}{2}=-3\)
b, Đặt \(f\left(x\right)=x^2-2\left(m-2\right)x+m^2-3m+5=0\)
\(f\left(-1\right)=\left(-1\right)^2-2\left(m-2\right)\left(-1\right)+m^2-3m+5=0\)
\(1+2\left(m-2\right)+m^2-3m+5=0\)
\(6+2m-4+m^2-3m=0\)
\(2-m+m^2=0\)( giải delta nhé )
\(\Delta=\left(-1\right)^2-4.2=1-8< 0\)
Vậy phương trình vô nghiệm
c, Để phương trình có nghiệm kép \(\Delta=0\)( tự giải :v )
a.
Phương trình có 2 nghiệm dương pb khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta'=\left(m+1\right)^2-\left(m+2\right)\left(m-4\right)>0\\x_1+x_2=\dfrac{2\left(m+1\right)}{m+2}>0\\x_1x_2=\dfrac{m-4}{m+2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m+9>0\\\dfrac{m+1}{m+2}>0\\\dfrac{m-4}{m+2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\m>-\dfrac{9}{4}\\\left[{}\begin{matrix}m>-1\\m< -2\end{matrix}\right.\\\left[{}\begin{matrix}m>4\\m< -2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>4\\-\dfrac{9}{4}< m< -2\end{matrix}\right.\)
b.
Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne-2\\\Delta'=4m+9\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne-2\\m\ge-\dfrac{9}{4}\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{m+2}\\x_1x_2=\dfrac{m-4}{m+2}\end{matrix}\right.\)
\(3\left(x_1+x_2\right)=5x_1x_2\)
\(\Leftrightarrow\dfrac{6\left(m+1\right)}{m+2}=\dfrac{5\left(m-4\right)}{m+2}\)
\(\Rightarrow6\left(m+1\right)=5\left(m-4\right)\)
\(\Leftrightarrow m=-26< -\dfrac{9}{4}\left(loại\right)\)
Vậy ko tồn tại m thỏa mãn yêu cầu
Đặt \(t=2^x>0\).
Phương trình ban đầu trở thành: \(t^2-2t+m=0\) (*)
Để phương trình ban đầu có 2 nghiệm phân biệt thì (*) phải có 2 nghiệm phân biệt dương: \(\left\{{}\begin{matrix}\Delta'>0\\t_1+t_2>0\\t_1t_2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}1-m>0\\2>0\left(đúng\right)\\m>0\end{matrix}\right.\Leftrightarrow0< m< 1\)
Đáp án B.
Đặt t = log2 x,
khi đó m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0
⇔ m + 1 t 2 + 2 t + m - 2 = 0 (*).
Để phương trình (*) có hai nghiệm phân biệt
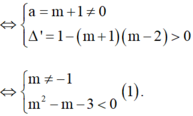
Khi đó gọi x1, x2 lần lượt hai nghiệm của phương trình (*).
Vì 0 < x1 < 1 < x2 suy ra
