Phương trình c o t 3 x = c o t x có mấy nghiệm thuộc 0 ; 10 π ?
A. 9
B. 20
C. 19
D. 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

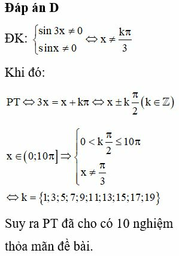

\(\text{Đặt f (x)= a.cos2x+b.sinx+cosx}\)
\(\text{Hàm f (x) xác định và liên tục trên R}\)
\(\text{f ( π /4 ) = b √2 /2 + √2 /2 }\)
\(\text{f ( 5/π4 ) = − b √ 2/ 2 − √ 2/ 2 }\)
\(\text{⇒ f (π /4) . f ( 5 π/ 4 ) = − 1/2 ( b + 1 )^ 2 ≤ 0 ; ∀ a ; b ; c}\)
\(⇒ f (x)= 0 luôn có ít nhất 1 nghiệm thuộc đoạn [ π /4 ; 5π/4]\)
Hay pt đã có nghiệm.

Thay \(x_1=-3\) vào pt ta được:
\(9-3m+m+3=0\Leftrightarrow2m=12\Rightarrow m=6\)
Khi đó nghiệm còn lại: \(x_2=-m-x_1=-6+3=-3\)
Khi pt có 2 nghiệm, theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=m+3\end{matrix}\right.\)
\(\Rightarrow x_1+x_2+x_1x_2=3\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m

2: \(\text{Δ}=\left(2m+6\right)^2-4\left(m^2-1\right)\)
\(=4m^2+24m+36-4m^2+4=24m+40\)
Để phương trình có hai nghiệm phân biệt thì 24m+40>0
hay m>-5/3
Để phương trình có hai nghiệm dương phân biệt thì:
\(\left\{{}\begin{matrix}-2m-6>0\\m^2-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< -3\\\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -3\)
=>m\(\in\varnothing\)
3: Để phương trình có hai nghiệm trái dấu thì (m-1)(m+1)<0
=>-1<m<1

b: x1=3x2 và x1+x2=2m-2
=>3x2+x2=2m-2 và x1=3x2
=>x2=0,5m-0,5 và x1=1,5m-1,5
x1*x2=-2m
=>-2m=(0,5m-0,5)(1,5m-1,5)
=>-2m=0,75(m^2-2m+1)
=>0,75m^2-1,5m+0,75+2m=0
=>\(m\in\varnothing\)
c: x1/x2=3
x1+x2=2m-2
=>x1=3x2 và x1+x2=2m-2
Cái này tương tự câu b nên kết quả vẫn là ko có m thỏa mãn

\(pt:x^2-2\left(m-1\right)x-m-3=0\)
\(\Delta=\left(2-2m\right)^2-4.\left(-m-3\right)=4-8m+4m^2+4m+12=4m^2-4m+16=\left(2m-2\right)^2+8>0\forall m\)
⇒ pt luôn có 2 nghiệm phân biệt
Theo hệ thức Vi-et:
\(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có: \(x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=\left(2m-2\right)^2-2.\left(-m-3\right)=4m^2-8m+4+2m+6=4m^2-6m+10\)
\(\Delta=\left(-6\right)^2-4.4.10=-124< 0\)
⇒ pt vô nghiệm nên không có m phù hợp
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-m-3\end{matrix}\right.\Leftrightarrow x_1+x_2+2x_1x_2=2m-2-2m-6\Leftrightarrow x_1+x_2+2x_1x_2=-8\)
⇒ Đây chính là hệ thức liên hệ giữa các nghiệm không phụ thuộc vào m