Question

[Pham Trong Bach]

Cho hàm số:  $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}\mathrm{x}+\mathrm{a}\mathrm{khi}\mathrm{x}<0\\ {\mathrm{x}}^2+1\mathrm{khi}\mathrm{x}\ge 0\end{array}\right.$. Xác định a để hàm số liên tục tại  ${\mathrm{x}}_0=0$.

A. a = 0

B. a = 2

C. a = -1

D. a = 1

Answer 1

[Cao Minh Tâm]

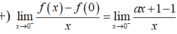
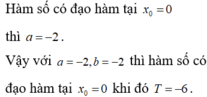
Đáp án D

Hàm số xác định với mọi  x ∈ ℝ .

Em có:  lim x → 0 + f x = lim x → 0 + x 2 + 1 = 1 lim x → 0 − f x = lim x → 0 − x + a = a  và f(0) = 1.

Vậy: nếu a = 1 thì  lim x → 0 + f x = lim x → 0 − f x = f 0 = 1 ⇒ hàm số liên tục tại  x 0 = 0 .

        nếu  a ≠ 1  thì  lim x → 0 + f x ≠ lim x → 0 − f x ⇒ hàm số gián đoạn tại  x 0 = 0 .