Làm giúp mình với
K
Khách
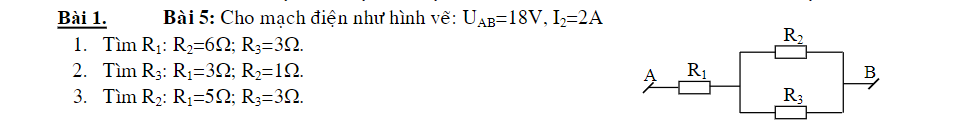
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
làm giúp mình với mình làm ơn đó ạ
18 tháng 10 2021
\(\dfrac{x}{-3}=\dfrac{y}{7}\Rightarrow\dfrac{x}{6}=\dfrac{y}{-14};\dfrac{y}{-2}=\dfrac{z}{5}\Rightarrow\dfrac{y}{-14}=\dfrac{z}{35}\\ \Rightarrow\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}=\dfrac{2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{-12+56+175}=\dfrac{146}{219}=\dfrac{2}{3}\\ \Rightarrow\left\{{}\begin{matrix}x=6\cdot\dfrac{2}{3}=4\\y=-14\cdot\dfrac{2}{3}=-\dfrac{28}{3}\\z=35\cdot\dfrac{2}{3}=\dfrac{70}{3}\end{matrix}\right.\)
25 tháng 12 2021
x/-3=y/7;y/-2=z/5 và -2x-4y+5z=146
BCNN(7,2)=14
=>x/-3=y/7;y/-2=z/5
=>x/-3=y/7=>x/6=y/14(1)
=>y/-2=z/5=>y/-14=z/35(2)
từ(1) và (2) =>x/6=y/-14=z/35 và -2x-4y+5z=146
Sử dụng tính chất dãy tỉ số bằng nhau:
=>x/6=y/-14=z/35=>-2x-4y+5z/(-2).6-4.(-14)+5.35=146/219=2/3
=>x/6=2/3=>x=2.6/3=4
=>y/-14=2/3=>y=-14.2/3=-28/3
=>z/35=2/3=>z=35.2/3=70/3
S2
1
20 tháng 5 2022
\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2
BH
1
DT
Đỗ Thanh Hải
CTVVIP
8 tháng 10 2021
1 How long do you live in HN
2 How often did you go to the movies
3 What did Mrs Robinson buy
4 When was your father in Nghe An
5 How do they go to school
6 Why didn't she go to class
7 Who left home at 7o'clock yesterday
8 What subject does he study in the high school
9 What is your favorite hobby
10 How far is it
RT
1
15 tháng 10 2023
1:
ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)
=>\(BC=\dfrac{9^2}{5.4}=15\left(cm\right)\)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
BC=BH+CH
=>CH=BC-BH=15-5,4=9,6cm
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot15=9\cdot12=108\)
=>AH=7,2(cm)
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF=7,2(cm)
Xét ΔABC vuông tại A có
\(sinABC=\dfrac{AC}{BC}=\dfrac{4}{5}\)
nên \(\widehat{ABC}\simeq53^0\)
=>\(\widehat{HAC}=\widehat{ABC}\simeq53^0\)
2:
ΔHAB vuông tại H có HE là đường cao
nên \(HE\cdot BA=HA\cdot HB\)
=>\(HE\cdot9=5.4\cdot7.2\)
=>\(HE=5.4\cdot0.8=4.32\left(cm\right)\)
ΔHAC vuông tại H có HF là đường cao
nên \(HF\cdot AC=HA\cdot HC\)
=>\(HF\cdot12=9.6\cdot7.2\)
=>\(HF=0.8\cdot7.2=5.76\left(cm\right)\)
\(S_{AEHF}=HE\cdot HF=5.76\cdot4.32=24.8832\left(cm^2\right)\)
\(S_{AEF}=\dfrac{1}{2}\cdot AE\cdot AF=\dfrac{1}{2}\cdot5.76\cdot4.32=12.4416\left(cm^2\right)\)
3: ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔHAC vuông tại H có FH là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AE\cdot AB=AF\cdot AC\)
4: \(AB\cdot cosB+AC\cdot cosC\)
\(=AB\cdot\dfrac{AB}{BC}+AC\cdot\dfrac{AC}{BC}\)
\(=\dfrac{AB^2+AC^2}{BC}=\dfrac{BC^2}{BC}=BC\)
6:
Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
CD
1
1. Tìm R1:
\(U_{23}=U_2=U_3=I_2\cdot R_2=2\cdot6=12V\left(R_2\backslash\backslash R_3\right)\)
\(I=I_1=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{12}{\dfrac{6.3}{6+3}}=6A\left(R_1ntR_{23}\right)\)
\(\Rightarrow R_1=\dfrac{U_1}{I_1}=\dfrac{\left(18-12\right)}{6}=1\Omega\)
2. Tìm R3:
\(U_{23}=U_2=U_3=I_2\cdot R_2=2.1=2V\left(R_2\backslash\backslash R_3\right)\)
\(U_1=U-U_{23}=18-2=16V\)
\(\rightarrow I=I_1=I_{23}=\dfrac{U_1}{R_1}=\dfrac{16}{3}=\dfrac{16}{3}A\left(R_1ntR_{23}\right)\)
\(\rightarrow I_3=I_{23}-I_2=\dfrac{16}{3}-2=\dfrac{10}{3}A\)
\(\Rightarrow R_3=\dfrac{U_3}{I_3}=\dfrac{2}{\dfrac{10}{3}}=0,6\Omega\)