Tính lim x → a x 4 - a 4 x - a .
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

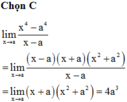

a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{3x^4}{x^4}-\dfrac{2x^5}{x^4}}{\dfrac{5x^4}{x^4}+\dfrac{x}{x^4}+\dfrac{4}{x^4}}=+\infty\)
b/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{x}{x}-\dfrac{1}{x}}{\sqrt{\dfrac{x^2}{x^2}-\dfrac{1}{x^2}}}=1\)

a/ \(\lim\limits_{x\rightarrow2}\dfrac{2+3}{4+2+4}=\dfrac{5}{10}=\dfrac{1}{2}\)
b/ \(\lim\limits_{x\rightarrow-3}\dfrac{\left(x+2\right)\left(x+3\right)}{x\left(x+3\right)}=\lim\limits_{x\rightarrow-3}\dfrac{x+2}{x}=\dfrac{-3+2}{-3}=\dfrac{1}{3}\)

a: \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{2x+10}-4}{3x-9}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2x+10-16}{3x-9}\cdot\dfrac{1}{\sqrt{2x+10}+4}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2\left(x-3\right)}{3\left(x-3\right)\cdot\left(\sqrt{2x+10}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{2}{3\left(\sqrt{2x+10}+4\right)}\)
\(=\dfrac{2}{3\cdot\sqrt{6+10}+3\cdot4}=\dfrac{2}{3\cdot4+3\cdot4}=\dfrac{2}{24}=\dfrac{1}{12}\)
b: \(\lim\limits_{x\rightarrow7}\dfrac{\sqrt{4x+8}-6}{x^2-9x+14}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4x+8-36}{\sqrt{4x+8}+6}\cdot\dfrac{1}{\left(x-2\right)\left(x-7\right)}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4x-28}{\left(\sqrt{4x+8}+6\right)\cdot\left(x-2\right)\left(x-7\right)}\)
\(=\lim\limits_{x\rightarrow7}\dfrac{4}{\left(\sqrt{4x+8}+6\right)\left(x-2\right)}\)
\(=\dfrac{4}{\left(\sqrt{4\cdot7+8}+6\right)\left(7-2\right)}\)
\(=\dfrac{4}{5\cdot12}=\dfrac{4}{60}=\dfrac{1}{15}\)
c: \(\lim\limits_{x\rightarrow5}\dfrac{x^2-8x+15}{2x^2-9x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{2x^2-10x+x-5}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(x-3\right)\left(x-5\right)}{\left(x-5\right)\left(2x+1\right)}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{x-3}{2x+1}=\dfrac{5-3}{2\cdot5+1}=\dfrac{2}{11}\)

a/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{x^2-x+1-x^2-x-1}{\sqrt{x^2-x+1}+\sqrt{x^2+x+1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{-\dfrac{2x}{x}}{\sqrt{\dfrac{x^2}{x^2}-\dfrac{x}{x^2}+\dfrac{1}{x^2}}+\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}+\dfrac{1}{x^2}}}=-\dfrac{2}{1+1}=-1\)
b/ \(=\lim\limits_{x\rightarrow2}\dfrac{4x+1-9}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4\left(x-2\right)}{\left(x-2\right)\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{4}{\left(x+2\right)\left(\sqrt{4x+1}+3\right)}=\dfrac{4}{\left(2+2\right)\left(\sqrt{4.2+1}+3\right)}=\dfrac{1}{6}\)
c/ \(=\lim\limits_{x\rightarrow-2}\dfrac{2x+5-1}{\left(x-2\right)\left(x+2\right)\left(\sqrt{2x+5}+1\right)}=\lim\limits_{x\rightarrow-2}\dfrac{2}{\left(x-2\right)\left(\sqrt{2x+5}+1\right)}=\dfrac{2}{\left(-2-2\right)\left(\sqrt[2]{2.\left(-2\right)+5}+1\right)}=\dfrac{2}{\left(-4\right).2}=-\dfrac{1}{4}\)

\(\lim\limits_{x\rightarrow-3}\dfrac{x^2-1}{x+1}=\dfrac{\left(-3\right)^2-1}{-3+1}=-4\) (câu này \(x\rightarrow-3\) hay \(x\rightarrow-1\) vậy?)
\(\lim\limits_{x\rightarrow-2}\dfrac{4-x^2}{x+2}=\lim\limits_{x\rightarrow-2}\dfrac{\left(2-x\right)\left(x+2\right)}{x+2}=\lim\limits_{x\rightarrow-2}\left(2-x\right)=4\)

a/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{x\sqrt{x^2+1}}{x}-\dfrac{2x}{x}+\dfrac{1}{x}}{\sqrt[3]{\dfrac{2x^3}{x^3}-\dfrac{2x}{x^3}}+\dfrac{1}{x}}=0\)
b/ \(=\lim\limits_{x\rightarrow-\infty}\dfrac{\dfrac{8x^7}{x^7}}{\dfrac{\left(-2x^7\right)}{x^7}}=-\dfrac{8}{2^7}\)
c/ \(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{4x^2}{x^2}+\dfrac{x}{x^2}}+\sqrt[3]{\dfrac{8x^3}{x^3}+\dfrac{x}{x^3}-\dfrac{1}{x^3}}}{\sqrt[4]{\dfrac{x^4}{x^4}+\dfrac{3}{x^4}}}=\dfrac{2+2}{1}=4\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{2x+2}+\sqrt{5x+4}-5}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt{2x+2}-2+\sqrt{5x+4}-3}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{2\left(x-1\right)}{\sqrt{2x+2}+2}+\dfrac{5\left(x-1\right)}{\sqrt{5x+4}+3}}{x-1}=\lim\limits_{x\rightarrow1}\left(\dfrac{2}{\sqrt{2x+2}+2}+\dfrac{5}{\sqrt{5x+4}+3}\right)=\dfrac{2}{2+2}+\dfrac{5}{3+3}=...\)
Đề câu b là \(...\sqrt{90-6x}\) hay \(\sqrt{9-6x}\) vậy em? Hình như cái sau mới có lý

\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x^2+1}-\left(x+1\right)}{2x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{\left(\sqrt{x^2+1}-\left(x+1\right)\right)\left(\sqrt{x^2+1}+x+1\right)}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2x}{x\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{-2}{\left(2x-1\right)\left(\sqrt{x^2+1}+x+1\right)}\)
\(=\dfrac{-2}{\left(0-1\right)\left(\sqrt{1}+1\right)}=1\)
a. \(\lim\limits_{x\rightarrow2}\dfrac{x-2}{x^2-4}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{x+2}=\dfrac{1}{4}\)
b. \(\lim\limits_{x\rightarrow3^-}\dfrac{x+3}{x-3}=\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}\)
Do \(\lim\limits_{x\rightarrow3^-}\left(-x-3\right)=-6< 0\)
\(\lim\limits_{x\rightarrow3^-}\left(3-x\right)=0\) và \(3-x>0;\forall x< 3\)
\(\Rightarrow\lim\limits_{x\rightarrow3^-}\dfrac{-x-3}{3-x}=-\infty\)