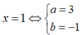Tìm a, b để hàm số f ( x ) = x 2 + x k h i x ≥ 1 a x + b k h i x < 1 có đạo hàm tại x = 1.
A. a = 23 b = - 1
B. a = 3 b = - 11
C. a = 33 b = - 31
D. a = 3 b = - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Parabol: \(y = a{(x - h)^2} + k\) với \(I(h;k) = \left( {\frac{5}{2}; - \frac{1}{4}} \right)\) là tọa độ đỉnh.
\( \Rightarrow y = a{\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4}\)
(P) đi qua \(A(1;2)\) nên \(2 = a{\left( {1 - \frac{5}{2}} \right)^2} - \frac{1}{4} \Rightarrow a = 1\)
\( \Rightarrow y = {\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4} \Leftrightarrow y = {x^2} - 5x + 6\)
Vậy parabol đó là \(y = {x^2} - 5x + 6\)
b) Vẽ parabol \(y = {x^2} - 5x + 6\)
+ Đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\)
+ Giao với Oy tại điểm \((0;6)\)
+ Giao với Ox tại điểm \((3;0)\) và \((2;0)\)
+ Trục đối xứng \(x = \frac{5}{2}\). Điểm đối xứng với điểm \((0;6)\) qua trục đối xứng có tọa độ \((5;6)\)

b) Hàm số đồng biến trên khoảng \(\left( { - \frac{5}{2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{5}{2}} \right)\)
c) \(f(x) \ge 0 \Leftrightarrow {x^2} - 5x + 6 \ge 0\)
Cách 1: Quan sát đồ thị, ta thấy các điểm có\(y \ge 0\) ứng với hoành độ \(x \in ( - \infty ;2] \cup [3; + \infty )\)
Do đó tập nghiệm của BPT \(f(x) \ge 0\) là \(S = ( - \infty ;2] \cup [3; + \infty )\)
Cách 2:
\(\begin{array}{l} \Leftrightarrow {x^2} - 5x + 6 \ge 0\\ \Leftrightarrow (x - 2)(x - 3) \ge 0\end{array}\)
Do đó \(x - 2\) và \(x - 3\) cùng dấu. Mà \(x - 2 > x - 3\;\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 \ge 0\\x - 2 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le 2\end{array} \right.\)
Tập nghiệm của BPT là \(S = ( - \infty ;2] \cup [3; + \infty )\)

Bài 1:
a) \(A=\frac{1}{2.5}+\frac{1}{5.8}+\frac{1}{8.11}+...+\frac{1}{2012.2015}\)
\(A=\frac{1}{3}.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{2012}-\frac{1}{2015}\right)\)
\(A=\frac{1}{3}.\left(\frac{1}{2}-\frac{1}{2015}\right)\)
\(A=\frac{1}{3}\cdot\frac{2013}{4030}=\frac{671}{4030}\)
Bài 2:
ta có: \(\frac{a}{b+c}=\frac{b}{a+c}=\frac{c}{a+b}\)
\(\Rightarrow\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=\frac{b+c+a+c+a+b}{a+b+c}=\frac{2a+2b+2c}{a+b+c}\)
\(=\frac{2.\left(a+b+c\right)}{a+b+c}=2\)
\(\Rightarrow\frac{b+c}{a}=\frac{a+c}{b}=\frac{a+b}{c}=2\)
\(\Rightarrow A=\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}=2+2+2=6\)
Bài 3:
a) f(1) = 4/1 = 4
=> f(1) = 4
g(-1) = (-1)^2 = 1
=> g(-1) = 1
h(-5) = -2.(-5)^2 - 5/(-5) = -2.25 + 1 = -50 + 1 = -49
=> h(-5) = -49
b) ta có: k(x)=f(x)+g(x)+h(x)
=> k(x) = 4/x + x^2 -2x^2 - 5/x
k(x) = - (5/x - 4/x) - (2x^2-x^2)
k(x) = -1/x - x
\(k_{\left(x\right)}=\frac{-1}{x}-\frac{x.x}{x}=\frac{-1-x^2}{x}\)
c) Để k(x) = 0
=> -1-x^2/x = 0 ( x khác 0)
=> -1-x^2 = 0
=> x^2 = -1
=> không tìm được x
Bài 4:
a) Xét tam giác ABC vuông tại A
có: góc B + góc C = 90 độ ( 2 góc phụ nhau)
thay số: 60 độ + góc C = 90 độ
góc C = 90 độ - 60 độ
góc C = 30 độ
=> AB = BC/2 ( cạnh đối diện với góc 30 độ)
thay số: 5 = BC/2
=> BC = 5.2
=> BC = 10 cm
Xét tam giác ABC vuông tại A
có: AC^2 + AB^2 = BC^2 ( py - ta - go)
thay số: AC^2 + 5^2 = 10^2
AC^2 + 25 = 100
AC^2 = 75
\(\Rightarrow AC=\sqrt{75}\) cm

Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
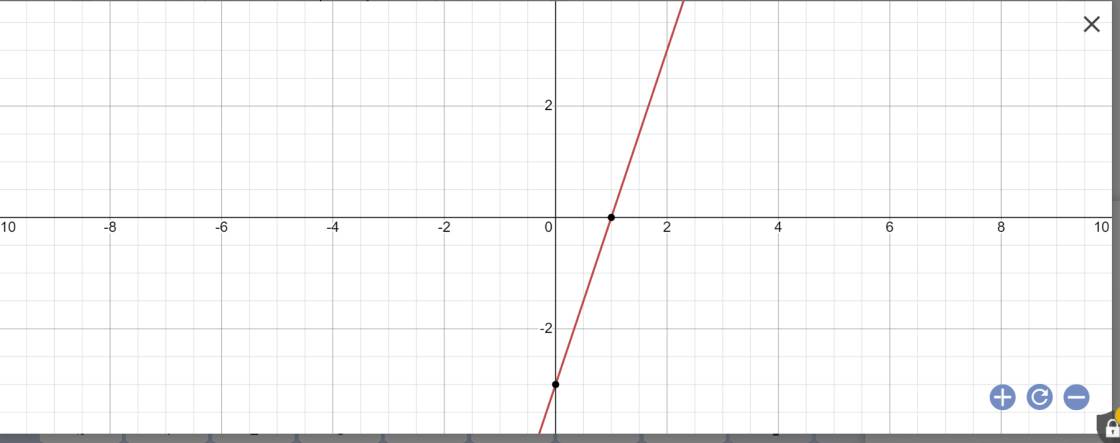
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2

a) \(f\left(x\right)=5x^3-7x^2+2x+5\)
\(\Rightarrow f\left(1\right)=5.1^3-7.1^2+2.1+5\)
\(\Rightarrow f\left(1\right)=5.1-7.1+2+5\)
\(\Rightarrow f\left(1\right)=5-7+7\)
\(\Rightarrow f\left(1\right)=5\)
Vậy f(1) = 5.
\(g\left(x\right)=7x^3-7x^2+2x+5\)
\(\Rightarrow g\left(\frac{1}{2}\right)=7.\left(\frac{1}{2}\right)^3-7.\left(\frac{1}{2}\right)^2+2.\frac{1}{2}+5\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=7.\frac{1}{8}-7.\frac{1}{4}+1+5\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{7}{8}-\frac{14}{8}+6\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{-7}{8}+\frac{48}{8}\)
\(\Leftrightarrow g\left(\frac{1}{2}\right)=\frac{41}{8}\)
Vậy \(g\left(\frac{1}{2}\right)=\frac{41}{8}\)
\(h\left(x\right)=2x^3+4x+1\)
\(\Rightarrow h\left(0\right)=2.0^3+4.0+1\)
\(\Rightarrow h\left(0\right)=0+0+1\)
\(\Rightarrow h\left(0\right)=1\)
Vậy \(h\left(0\right)=1\)

Bài 6 : Tìm x thuộc Z để giá trị của biểu thức: x^3+2x-x^2+7 chia hết cho giá trị của biểu thức x^2 + 1

Bài 7: Tìm a, b để đa thức: x^3+ax+b chia hết cho x^2+2x-2

Đáp án D
- Ta có:
- Hàm có đạo hàm tại thì hàm liên tục tại x = 1 ⇔ a + b = 2 (1)
- Hàm có đạo hàm tại