Cho hai đường thẳng song song d1; d2. Trên d1 có 6 điểm phân biệt được tô màu đỏ. Trên d2 có 4 điểm phân biêt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Vì $(d_1)\parallel (d_2)$ nên $a=1$
$A\in (d_1)$ nên $y_A=ax_A+b\Leftrightarrow 2=a(-1)+b$
$\Leftrightarrow b=2+a=2+1=3$
Vậy $a=1; b=3$

b: \(y_N=-\dfrac{3}{4}:3-\dfrac{1}{2}=\dfrac{-1}{4}-\dfrac{1}{2}=-\dfrac{3}{8}\)
Vì (d)//(d1) nên a=-1
Vậy: (d): y=-x+b
Thay x=3/4 và y=-3/8 vào (d), ta được:
b-3/4=-3/8
hay b=3/8

Hai đường thẳng song song khi m 3 = 2 − 4 ≠ − 3 2 n ê n m = − 3 2
Chọn đáp án C.

Giải
d1 và d2 là 2 đường thẳng trùng nhau vì:
+ Có một và chỉ một đường thẳng phân biệt vs đường thẳng đó
+ Có vô số đường thẳng trùng nhau song song với đường thẳng đó
x y O d1 d2
Cho hai đường thẳng:
d1: mx + y = m + 1
d2: x + my = 2
Điều kiện của m để hai đường thẳng song song là:

Chọn C.
d1 song song với d2 khi và chỉ khi 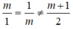 khi đó ta có:
khi đó ta có:
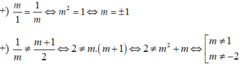
Vậy m = -1.

Chọn C
* Số tam giác có 2 đỉnh thuộc
d
1
và 1 đỉnh thuộc
d
2
là: ![]() .
.
* Số tam giác có 1 đỉnh thuộc
d
1
và 2 đỉnh thuộc
d
2
là: ![]() .
.
Vậy có 70 + 105 = 175 tam giác.

Gọi pt d2 có dạng \(y=ax+b\)
Do d2 qua A và B nên ta có:
\(\left\{{}\begin{matrix}a+b=2\\-3a+b=-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\) \(\Rightarrow d_2:y=x+1\)
Do \(d_1\) song song \(d_2\) nên chúng có cùng hệ số góc
\(\Rightarrow k=1\)

Để hai đường thẳng song song mà không trùng nhau thì điều kiện cần và đủ là :
\(\hept{\begin{cases}m=1\\3m+2\ne1\end{cases}\Leftrightarrow\hept{\begin{cases}m=1\\m\ne-\frac{1}{3}\end{cases}\Leftrightarrow}m=1}\)
Đáp án B
Số tam giác được tạo bởi 2 đỉnh trên d1 và 1 đỉnh trên d2 là: C 6 2 . C 4 1 = 60 . Số tam giác được tạo bởi 1 đỉnh trên d1 và 2 đỉnh trên d2 là: C 6 1 . C 4 2 = 36 . Do đó số tam giác được tạo thành là: 60 + 36 = 96. Xác suất cần tìm là: 60 96 = 5 8 .