Tìm m để phương trình 2sinx + mcosx = 1 - m (1) có nghiệm .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
f ' x = 0 ⇔ 2 cos x − m sin x = 3 *
Phương trình
f ' x = 0 ⇔ 2 cos x − m sin x = 3 *
Để (*) có nghiệm khi và chỉ khi
3 2 2 + − m 2 ≤ 1 ⇔ m 2 ≥ 5 ⇔ m ≤ 5

1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

Đáp án C
để phương trình: 2sinx + mcosx - 2m = 0 có nghiệm
2 2 + m 2 ≥ 2 m 2 ⇔ m 2 ≤ 4 3 ⇔ - 2 3 ≤ m ≤ 2 3
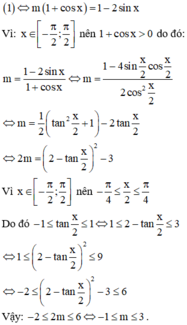
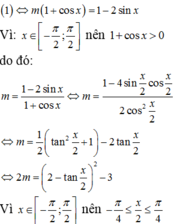
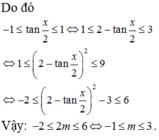
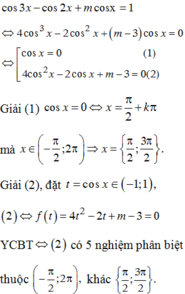
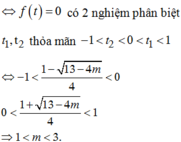
Chọn D
Do đó